题目内容
4.已知代数式x2+ax+6-2bx2+x-1的值与字母x的取值无关,又A=-a2+ab-2b2,B=3a2-ab+3b2.求:3A+[(A+3B)-2(A+B)]的值.分析 由已知代数式的值与x取值无关,求出a与b的值,原式去括号合并后,将A与B代入化简得到最简结果,把a与b的值代入计算即可求出值.
解答 解:∵代数式x2+ax+6-2bx2+x-1=(1-2b)x2+(a+1)x+5的值与字母x的取值无关,
∴1-2b=0,a+1=0,
解得:a=-1,b=$\frac{1}{2}$,
∵A=-a2+ab-2b2,B=3a2-ab+3b2,
∴原式=3A+A+3B-2A-2B=2A+B=-2a2+2ab-4b2+3a2-ab+3b2=a2+ab-b2=1-$\frac{1}{2}$-$\frac{1}{4}$=$\frac{1}{4}$.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 如图,将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm和$\sqrt{300}$cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是( )
如图,将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm和$\sqrt{300}$cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是( )
 如图,将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm和$\sqrt{300}$cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是( )
如图,将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm和$\sqrt{300}$cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 7cm |
12.下列代数式:是单项式为( )
| A. | $\frac{b}{a}$ | B. | $\frac{x-y}{5}$ | C. | 2π | D. | x+1 |
16.如果两个数的和是10,其中一个数用字母x表示,那么表示这两个数的积的代数式是( )
| A. | 10x | B. | x(10+x) | C. | x(10-x) | D. | x(x-10) |
13.下列结论正确的是( )
| A. | 0是正数也是有理数 | |
| B. | 两数之积为正,这两数同为正 | |
| C. | 几个数相乘,积的符号由负因数的个数决定 | |
| D. | 互为相反数的两个数的绝对值相等 |
 如图所示的运算程序中,若开始输入的x值为36,我们发现第1次输出的结果为18,第2次输出的结果为9,…第2015次输出的结果为3.
如图所示的运算程序中,若开始输入的x值为36,我们发现第1次输出的结果为18,第2次输出的结果为9,…第2015次输出的结果为3.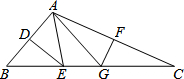 在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.若∠BAC=106°,则∠EAG=32°.
在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.若∠BAC=106°,则∠EAG=32°.