题目内容
12.计算:(1)$\sqrt{18}$$+\frac{1}{5}$$\sqrt{50}$-4$\sqrt{\frac{1}{2}}$
(2)$\frac{\sqrt{72}-\sqrt{24}}{\sqrt{8}}$-(2+$\sqrt{3}$)2.
分析 (1)先进行二次根式的化简,然后合并;
(2)先进行二次根式的化简以及完全平方公式,然后合并.
解答 解:(1)原式=3$\sqrt{2}$+$\sqrt{2}$-2$\sqrt{2}$
=2$\sqrt{2}$;
(2)原式=$\sqrt{9}$-$\sqrt{3}$-7-4$\sqrt{3}$
=-4-5$\sqrt{3}$.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的化简以及同类二次根式的合并.

练习册系列答案
相关题目
3.我市政府为响应党中央建设社会主义新农村和节约型社会的号召,决定资助部分农村地区修建一批沼气池,使农民用到经济、环保的沼气能源.红星村共有264户村民,村里得到34万元的政府资助款,不足部分由村民集资解决.修建A型、B型沼气池共20个.两种型号沼气池每个修建费用、可供使用的户数、修建用地情况见下表:
政府土地部门只批给该村沼气池修建用地708m2.若修建A型沼气池x个,修建两种型号沼气池共需费用y万元.
(1)求y与x之间的函数关系式;
(2)既不超过政府批给修建沼气池用地面积,又要使该村每户村民用上沼气的修建方案有几种?
(3)若平均每户村民集资700元,能否满足所需费用最少的修建方案?
| 沼气池 | 修建费用(万元/个) | 可供使用户数(户/个) | 占地面积(m2/个) |
| A型 | 3 | 20 | 48 |
| B型 | 2 | 3 | 6 |
(1)求y与x之间的函数关系式;
(2)既不超过政府批给修建沼气池用地面积,又要使该村每户村民用上沼气的修建方案有几种?
(3)若平均每户村民集资700元,能否满足所需费用最少的修建方案?
20.小芳测得连续五天日最低气温并整理后得出下表:
由于不小心被墨迹污染了一个数据,这个数据是2.
| 日期 | 一 | 二 | 三 | 四 | 五 | 平均气温 | 方差 |
| 最低气温 | 1 | 3 | 2 | 5 | 4 | 3 |  |
7.已知3x=4y,则$\frac{x}{y}$的值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{7}$ | D. | $\frac{3}{7}$ |
17.世界人口统计表
(1)根据表中的数据,在直角坐标系中画出世界人口增长曲线图;
(2)选择一个近似于人口增长曲线的一次函数,写出它的解析式;
(3)按照这样的增长趋势,估计2020年的世界人口数.
| 年份x | 1960 | 1974 | 1987 | 1999 | 2010 |
| 人口数y/亿 | 30 | 40 | 50 | 60 | 69 |
(2)选择一个近似于人口增长曲线的一次函数,写出它的解析式;
(3)按照这样的增长趋势,估计2020年的世界人口数.
4.已知直线y=2x与y=-x+b的交点为(-1,a),则方程组$\left\{\begin{array}{l}{y-2x=0}\\{y+x-b=0}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ |
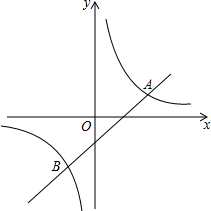 如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象相交于A(2,1),B两点.
如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象相交于A(2,1),B两点.