计算:(1)b2•bm•bm-1 (2)(-3a6)2+(-2a3)3•a3．题目和参考答案——青夏教育精英家教网—

题目内容

2．计算：
（1）b²•b^m•b^m-1
（2）（-3a⁶）²+（-2a³）³•a³．

分析（1）根据同底数幂的乘法法则解答即可．
（2）根据整式的混合运算顺序，首先计算乘方和乘法，然后计算加法，求出算式的值是多少即可．

解答解：（1）b²•b^m•b^m-1
=b^2+m+m-1
=b^2m+1．

（2）（-3a⁶）²+（-2a³）³•a³
=9a¹²-8a¹²
=a¹²．

点评（1）此题主要考查了整式的混合运算，要熟练掌握，解答此题的关键是要明确：有乘方、乘除的混合运算中，要按照先乘方后乘除的顺序运算，其运算顺序和有理数的混合运算顺序相似．
（2）此题还考查了幂的乘方和积的乘方的运算方法，以及同底数幂的乘法法则，要熟练掌握．

练习册系列答案

13．已知等式$\sqrt{4{a}^{2}-8a+4}$+2a=2，则能使等式成立的a的取值范围为a≤1．

10．下列图形“线段、角、等腰三角形、平行四边形、圆”，其中既是轴对称图形，又是中心对称图形的有（　　）

17．在求1+6+6²+6³+6⁴+6⁵+6⁶+6⁷+6⁸+6⁹的值时，小林发现：从第二个加数起每一个加数都是前一个加数的6倍，于是她设：
S=1+6+6²+6³+6⁴+6⁵+6⁶+6⁷+6⁸+6⁹①然后在①式的两边都乘以6，得：
6S=6+6²+6³+6⁴+6⁵+6⁶+6⁷+6⁸+6⁹+6¹⁰②
②-①得6S-S=6¹⁰-1，即5S=6¹⁰-1，所以S=$\frac{{6}^{10}-1}{5}$，得出答案后，爱动脑筋的小林想：如果把“6”换成字母“a”（a≠0且a≠1），能否求出1+a+a²+a³+a⁴+…+a²⁰¹⁴的值？你的答案是（　　）

A．

$\frac{{a}^{2014}-1}{a-1}$

B．

$\frac{{a}^{2015}-1}{a-1}$

C．

$\frac{{a}^{2014}-1}{a}$

D．

a²⁰¹⁴-1

7．函数y=$\sqrt{x-8}$中自变量x的取值范围是（　　）

14．某电子厂商投产一种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数y=-2x+100．（利润=售价-制造成本）
（1）写出每月的利润z（万元）与销售单价x（元）之间的函数关系式；
（2）当销售单价为多少元时，厂商每月能获得350万元的利润？当销售单价为多少元时，厂商每月能获得最大利润？最大利润是多少？
（3）根据相关部门规定，这种电子产品的销售单价不能高于32元，如果厂商要获得每月不低于350万元的利润，那么制造出这种产品每月的最低制造成本需要多少万元？

11．下列分式中，不属于最简分式的，请在括号内写出化简后的结果，否则请在括号内打“√”．
①$\frac{4}{2x}$× ②$\frac{2x}{{x}^{2}+1}$√ ③$\frac{x-1}{{x}^{2}-1}$× ④$\frac{1-x}{x-1}$× ⑤$\frac{{a}^{2}+{b}^{2}}{a+b}$√．

12．

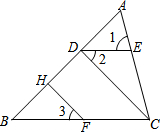已知，如图，DE∥BC，∠A=60°，∠B=50°；
（1）求∠1的度数；
（2）若FH⊥AB于点H，且∠2=∠3，试判断CD与AB的位置关系？并加以证明．

试题分类