题目内容
20.小芳测得连续五天日最低气温并整理后得出下表:| 日期 | 一 | 二 | 三 | 四 | 五 | 平均气温 | 方差 |
| 最低气温 | 1 | 3 | 2 | 5 | 4 | 3 |  |
分析 根据方差的计算公式求得方差即可.
解答 解:S2=$\frac{1}{5}$[(1-3)2+(3-3)2+(2-3)2+(4-3)2+(5-3)2]=2.
故答案为:2.
点评 本题考查了方差的定义.一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
相关题目
8.化简$\frac{{\sqrt{2}+\sqrt{5}-\sqrt{3}}}{{2\sqrt{30}-6\sqrt{2}+4\sqrt{3}}}$的结果是( )
| A. | $2\sqrt{6}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{6}}}{6}$ | D. | $\frac{{\sqrt{6}}}{12}$ |
5.若式子$\sqrt{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x≠2 | D. | x≥0 |
9.某电脑公司有A,B,C三种型号的电脑,其相应的价格如表:
已知某中学现有资金100500元,计划全部用于从这家电脑公司购进36台两种不同型号的电脑.请设计出几种不同的购买方案供该校选择,并说明理由.
| 型号 | A | B | C |
| 单价(元/台) | 6000 | 4000 | 2500 |
10.下列图形“线段、角、等腰三角形、平行四边形、圆”,其中既是轴对称图形,又是中心对称图形的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
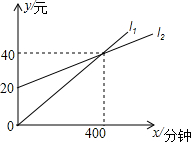 一家电信公司提供两种手机的月通话收费方式供用户选择,其中一种有月租费,另一种无月租费.这两种收费方式的通话费用y(元)与通话时间x(分钟)之间的函数关系如图所示.小红根据图象得出下列结论:
一家电信公司提供两种手机的月通话收费方式供用户选择,其中一种有月租费,另一种无月租费.这两种收费方式的通话费用y(元)与通话时间x(分钟)之间的函数关系如图所示.小红根据图象得出下列结论: 如图,在平面直角坐标系xOy中,⊙P的圆心P为(-3,a),⊙P与y轴相切于点C.直线y=-x被⊙P截得的线段AB长为4$\sqrt{2}$,则过点P的双曲线的解析式为y=-$\frac{3\sqrt{2}+9}{x}$.
如图,在平面直角坐标系xOy中,⊙P的圆心P为(-3,a),⊙P与y轴相切于点C.直线y=-x被⊙P截得的线段AB长为4$\sqrt{2}$,则过点P的双曲线的解析式为y=-$\frac{3\sqrt{2}+9}{x}$. 三个大小相同的球恰好放在一个圆柱体盒子里,三个球的体积之和占整个盒子容积的几分之几.(V球=$\frac{4}{3}π{r^3}$)
三个大小相同的球恰好放在一个圆柱体盒子里,三个球的体积之和占整个盒子容积的几分之几.(V球=$\frac{4}{3}π{r^3}$)