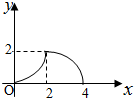题目内容
17.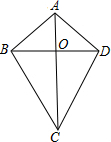 如图,四边形ABCD中,AB=AD,CB=CD,则称该四边形为“筝形”.连接对角线AC、BD,交于点O.
如图,四边形ABCD中,AB=AD,CB=CD,则称该四边形为“筝形”.连接对角线AC、BD,交于点O.(1)写出关于筝形对角线的一个性质BD⊥AC,且AC平分BD,并说明理由;
(2)给出下列四个条件:①OA=OC,②AC⊥BD,③∠ABD=∠CBD,④AB∥CD.从中选择一个条件①(填序号),使该筝形为菱形,并证明之.
分析 (1)证明△ABC≌△ADC,即可证得BD⊥AC,且AC平分BD;
(2)答案不唯一,选择①,根据“四条边相等的四边形为菱形”进行证明.
解答 解:(1)BD⊥AC,且AC平分BD.
理由如下:在△ABC与△ADC中,$\left\{\begin{array}{l}{AB=AD}\\{AC=AC}\\{BC=DC}\end{array}\right.$,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC.
又∵AB=AD,
∴AC⊥BD,OB=OD;
故答案是:BD⊥AC,且AC平分BD;
(2)选择①,理由如下:
∵BD⊥AC,OA=OC,
∴BC=AB.
又∵AB=AD,BC=CD,
∴AB=BC=CD=DA,
∴四边形ABCD为菱形.
故答案是:①.
点评 本题考查了菱形的判定,全等三角形的判定与性质.四条边都相等的四边形是菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知正六边形ABCDEF的边心距为$\sqrt{3}$cm,则正六边形的半径为( )cm.
| A. | 2$\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 4 |
2.在?ABCD中,∠A:∠B:∠C:∠D的值可以是( )
| A. | 1:2:3:4 | B. | 1:3:3:1 | C. | 3:3:1:1 | D. | 3:1:3:1 |
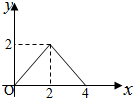
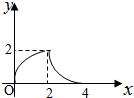
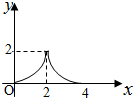
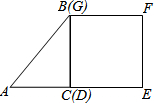 如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一条直线上,开始时点C与点D重合.将△ABC沿直线DE向右平移,直到点A与点E重合为止.设CD的长为x,若△ABC与正方形DEFG重合部分的面积为y,则y与x的函数图象是( )
如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一条直线上,开始时点C与点D重合.将△ABC沿直线DE向右平移,直到点A与点E重合为止.设CD的长为x,若△ABC与正方形DEFG重合部分的面积为y,则y与x的函数图象是( )