题目内容
2.在?ABCD中,∠A:∠B:∠C:∠D的值可以是( )| A. | 1:2:3:4 | B. | 1:3:3:1 | C. | 3:3:1:1 | D. | 3:1:3:1 |
分析 根据平行四边形的性质得到∠A=∠C,∠B=∠D,∠B+∠C=180°,∠A+∠D=180°,根据以上结论即可选出答案.
解答  解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,AB∥CD,
∴∠B+∠C=180°,∠A+∠D=180°,
即∠A和∠C的数相等,∠B和∠D的数相等,且∠B+∠C=∠A+∠D.
故选D.
点评 本题主要考查了平行四边形的性质,能根据平行四边形的对角相等及平行线的性质进行判断是解此题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
12.下列说法正确的个数有( )
①2是8的立方根; ②±4是64的立方根; ③无限小数都是无理数; ④带根号的数都是无理数.
①2是8的立方根; ②±4是64的立方根; ③无限小数都是无理数; ④带根号的数都是无理数.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.下列二次根式与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{45}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\sqrt{6}$ |
7.在四边形ABCD中,AD∥BC,∠B=∠C,要使四边形ABCD为矩形,还需添加一个条件,这个条件可以是( )
| A. | AB=CD | B. | AC=BD | C. | ∠A=∠D | D. | ∠A=∠B |
11.在?ABCD中,如果添加一个条件,就可推出?ABCD是矩形,那么添加的条件可以是( )
| A. | AB=BC | B. | AC=BD | C. | AC⊥BD | D. | AB⊥BD |
12.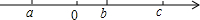 实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )
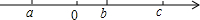 实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,下列式子中正确的是( )| A. | -a<b<c | B. | ab<ac | C. | -a+b>-a+c | D. | |a-b|<|a-c| |
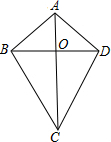 如图,四边形ABCD中,AB=AD,CB=CD,则称该四边形为“筝形”.连接对角线AC、BD,交于点O.
如图,四边形ABCD中,AB=AD,CB=CD,则称该四边形为“筝形”.连接对角线AC、BD,交于点O.