题目内容
17.已知关于x的方程x2-3x+2-m2=0(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程有一个根是-1,求m得值及方程的另一个根.
分析 (1)若方程有两个不相等的实数根,则应有△=b2-4ac>0,故计算方程的根的判别式即可证明方程根的情况;
(2)直接代入x=-1,求得m的值后,解方程即可求得另一个根.
解答 (1)证明:∵a=1,b=3,c=2-m2,
∴△=32-4×1×(2-m2)=4m2+1,
∵无论m取何值,m2≥0,
∴4m2+1>0,即△>0,
∴对于任意实数m,方程总有两个不相等的实数根.
(2)解:把x=-1代入原方程得1+3+2-m2=0
解得m=±$\sqrt{6}$,
故原方程化为x2-3x-4=0,
解得:x1=-1,x2=4,
即另一个根为x=4.
点评 本题是对根的判别式与根与系数关系的综合考查,一元二次方程根的情况与判别式△的关系:(1)△>0方程有两个不相等的实数根;(2)△=0方程有两个相等的实数根;(3)△<0方程没有实数根.

练习册系列答案
相关题目
7.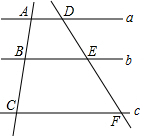 如图,已知a∥b∥c,AC=6,AB=2,EF=5,则DF的值为( )
如图,已知a∥b∥c,AC=6,AB=2,EF=5,则DF的值为( )
 如图,已知a∥b∥c,AC=6,AB=2,EF=5,则DF的值为( )
如图,已知a∥b∥c,AC=6,AB=2,EF=5,则DF的值为( )| A. | $\frac{5}{3}$ | B. | $\frac{5}{2}$ | C. | $\frac{10}{3}$ | D. | $\frac{15}{2}$ |
8. 如图,在?ABCD中,AC与BD交于点O,下列说法正确的是( )
如图,在?ABCD中,AC与BD交于点O,下列说法正确的是( )
 如图,在?ABCD中,AC与BD交于点O,下列说法正确的是( )
如图,在?ABCD中,AC与BD交于点O,下列说法正确的是( )| A. | AC=BD | B. | AC⊥BD | C. | AO=CO | D. | AB=BC |
12. 如图,△ABC的三个顶点分别为A(1,2),B(1,3),C(3,1).若反比例函数$y=\frac{k}{x}$在第一象限内的图象与△ABC有公共点,则k的取值范围是( )
如图,△ABC的三个顶点分别为A(1,2),B(1,3),C(3,1).若反比例函数$y=\frac{k}{x}$在第一象限内的图象与△ABC有公共点,则k的取值范围是( )
 如图,△ABC的三个顶点分别为A(1,2),B(1,3),C(3,1).若反比例函数$y=\frac{k}{x}$在第一象限内的图象与△ABC有公共点,则k的取值范围是( )
如图,△ABC的三个顶点分别为A(1,2),B(1,3),C(3,1).若反比例函数$y=\frac{k}{x}$在第一象限内的图象与△ABC有公共点,则k的取值范围是( )| A. | 2≤k≤3 | B. | 2≤k≤4 | C. | 3≤k≤4 | D. | 2≤k≤3.5 |
2.下列几组数中,能作为直角三角形三边长度的是( )
| A. | 2,3,4 | B. | 4,5,6 | C. | 6,8,11 | D. | 5,12,13 |
9.用配方法解方程x2-2x-3=0,原方程应变形为( )
| A. | (x-1)2=2 | B. | (x+1)2=4 | C. | (x-1)2=4 | D. | (x+1)2=2 |