题目内容
3. 如图,A在O正北方向,B在O正东方向,且A、B到点O的距离相等,甲从A出发,以每小时60千米的速度朝正东方向行驶,乙从B出发,以每小时40千米的速度朝正北方向行驶,1小时后,位于点O处的观察员发现甲乙两人之间的夹角为45°,此时甲乙两人相距( )千米.
如图,A在O正北方向,B在O正东方向,且A、B到点O的距离相等,甲从A出发,以每小时60千米的速度朝正东方向行驶,乙从B出发,以每小时40千米的速度朝正北方向行驶,1小时后,位于点O处的观察员发现甲乙两人之间的夹角为45°,此时甲乙两人相距( )千米.| A. | 80 | B. | 50$\sqrt{2}$ | C. | 100$\sqrt{2}$ | D. | 100 |
分析 利用旋转的性质结合全等三角形的判定与性质得出△COD≌△B′OC(SAS),则B′C=DC进而求出即可.
解答  解:由题意可得:AB′=BD=40千米,AC=60千米,
解:由题意可得:AB′=BD=40千米,AC=60千米,
将△OBD顺时针旋转270°,则BO与AO重合,
在△COD和△B′OC中
∵$\left\{\begin{array}{l}{DO=OB′}\\{∠COD=∠B′OC}\\{CO=CO}\end{array}\right.$,
∴△COD≌△B′OC(SAS),
则B′C=DC=40+60=100(千米),
故选:D.
点评 此题主要考查了勾股定理的应用以及全等三角形的判定与性质,得出△COD≌△B′OC是解题关键.

练习册系列答案
相关题目
14.中百超市的收银台平均每小时有60名顾客前来排队付款,每个收银台每小时能应付80名顾客付款.某天某时刻,超市如果只开设一个收银台.付款开始2小时就没有顾客排队,如果当时就开设两个收银台,付款开始( )小时就没有人排队.
| A. | 1 | B. | 0.8 | C. | 0.6 | D. | 0.4 |
11. 如图,△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,则OE:OB=( )
如图,△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,则OE:OB=( )
 如图,△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,则OE:OB=( )
如图,△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,则OE:OB=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
18.如图,已知点A表示的数是$\frac{1}{2}$,则点B表示的数是( )
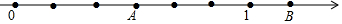
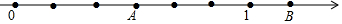
| A. | $1\frac{1}{3}$ | B. | $1\frac{1}{4}$ | C. | $1\frac{1}{5}$ | D. | $1\frac{1}{6}$ |
 在Rt△ABC中,∠A=90°,
在Rt△ABC中,∠A=90°,