题目内容
10.计算.(1)($\sqrt{45}$+$\sqrt{18}$)-($\sqrt{8}$-$\sqrt{125}$)
(2)(3$\sqrt{48}$-2$\sqrt{27}$)÷$\sqrt{6}$-$\frac{1}{2}$$\sqrt{32}$.
分析 (1)先把各二次根式化为最简二次根式,然后去括号后合并即可;
(2)先把各二次根式化为最简二次根式,再把括号内合并后进行二次根式的除法运算,然后进行二次根式的减法运算.
解答 解:(1)原式=3$\sqrt{5}$+3$\sqrt{2}$-2$\sqrt{2}$+5$\sqrt{5}$
=8$\sqrt{5}$+$\sqrt{2}$;
(2)原式=(12$\sqrt{3}$-6$\sqrt{3}$)÷$\sqrt{6}$-2$\sqrt{2}$
=6$\sqrt{3}$÷$\sqrt{6}$-2$\sqrt{2}$
=3$\sqrt{2}$-2$\sqrt{2}$
=$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
2.正比例函数y1=k1x的图象和反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,3)、B(1,-3)两点,若y1<y2,则x的取值范围是( )
| A. | x<-1或x>1 | B. | -1<x<0或x>1 | C. | x<-1或0<x<1 | D. | -1<x<0或 0<x<1 |
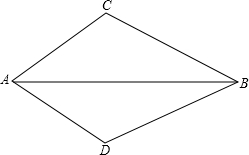 利用构造全等直角三角形证线段相等:如图,∠C=∠D,AC=AD,求证:BC=BD.
利用构造全等直角三角形证线段相等:如图,∠C=∠D,AC=AD,求证:BC=BD. 如图,三角形A′B′C′是由三角形ABC沿射线AC方向平移2cm得到的,若AC=3cm,则B′C=1cm.
如图,三角形A′B′C′是由三角形ABC沿射线AC方向平移2cm得到的,若AC=3cm,则B′C=1cm.