题目内容
20.有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.(1)问加工成的正方形零件的边长是多少mm?小颖善于反思,她又提出了如下的问题.
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,
这个矩形零件的两条边长又分别为多少mm?请计算.
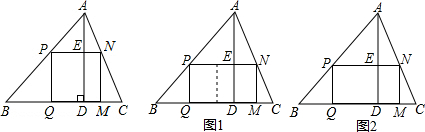
分析 (1)设正方形的边长为xmm,则PN=PQ=ED=x,AE=AD-ED=80-x,通过证明△APN∽△ABC,利用相似比可得到$\frac{x}{120}$=$\frac{80-x}{80}$,然后根据比例性质求出x即可;
(2)由于矩形是由两个并排放置的正方形所组成,则可设PQ=x,则PN=2x,AE=80-x,然后与(1)的方法一样求解.
解答 解:(1)设正方形的边长为xmm,则PN=PQ=ED=x,
∴AE=AD-ED=80-x,
∵PN∥BC,
∴△APN∽△ABC,
∴$\frac{PN}{BC}$=$\frac{AE}{AD}$,即$\frac{x}{120}$=$\frac{80-x}{80}$,解得x=48,
∴加工成的正方形零件的边长是48mm;
(2)设PQ=x,则PN=2x,AE=80-x,
∵PN∥BC,
∴△APN∽△ABC,
∴$\frac{PN}{BC}$=$\frac{AE}{AD}$,即$\frac{2x}{120}$=$\frac{80-x}{80}$,解得x=$\frac{240}{7}$,
∴2x=$\frac{480}{7}$,
∴这个矩形零件的两条边长分别为$\frac{240}{7}$mm,$\frac{480}{7}$mm.
点评 本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等计算相应线段的长.

练习册系列答案
相关题目
10.下列各数属于正数的是( )
| A. | 0 | B. | -1.2 | C. | -5 | D. | 7 |
11.根式$\sqrt{x-1}$有意义,则x满足( )
| A. | x>1 | B. | x<-1 | C. | x≥1 | D. | x≤-1 |
5.已知a=5,|b|=2,则a+b的值为( )
| A. | 7或3 | B. | ±7 | C. | ±3 | D. | 3或-7 |
9.下列说法错误的是( )
| A. | 锐角三角形的三条高线、三条中线、三条角平分线分别交于一点 | |
| B. | 钝角三角形有两条高线在三角形外部 | |
| C. | 直角三角形只有一条高线 | |
| D. | 任意三角形都有三条高线、三条中线、三条角平分线 |
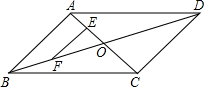 如图,?ABCD的对角线AC、BD相较于点O,点E、F分别是线段AO、BO的中点,若EF=3,△COD的周长是18,则?ABCD的两条对角线的和是( )
如图,?ABCD的对角线AC、BD相较于点O,点E、F分别是线段AO、BO的中点,若EF=3,△COD的周长是18,则?ABCD的两条对角线的和是( )