题目内容
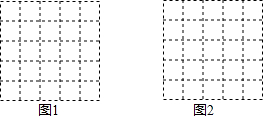所谓格点三角形指的是三角形的三个顶点均在正方形的格点上的三角形，在一个由5×5个边长为1的小正方形组成的正方形格点中．画出符合要求的格点三角形．（1）在图1中画一个面积为5的等腰直角三角形．
（2）在图2中画一个面积最大且腰长为有理数的等腰锐角三角形．
考点：勾股定理
专题：作图题
分析：（1）根据等腰直角三角形的性质求出直角边的长度，再利用勾股定理作出即可；
（2）根据勾股定理，作出腰长为5的等腰三角形即可．
（2）根据勾股定理，作出腰长为5的等腰三角形即可．
解答：解：（1）设等腰直角三角形直角边为a，
则
a2=5，
解得a=
，如图所示；
（2）如图所示，等腰三角形的腰长为5．
则
| 1 |
| 2 |
解得a=
| 10 |
（2）如图所示，等腰三角形的腰长为5．
点评：本题考查了勾股定理，等腰直角三角形的性质，等腰三角形的性质，熟记定理以及相关三角形的性质是解题的关键．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
在△ABC中，∠C=90°，CD是AB边上的高，则CD：CB=（ ）
| A、sinA | ||
| B、cosA | ||
| C、tanA | ||
D、
|
如图，在平面直角坐标系xOy中，A（-1，5），B（-2，0），C（-4，3）．
如图，已知直线y=
如图，将边长为2的正方形ABCD的各边四等分，把一长度为| 34 |
| A、CR3 |
| B、R1D |
| C、R2R3 |
| D、R2R1 |
如图，对称轴平行于y轴的抛物线与x轴交于（2，0），（6，0）两点，则它的对称轴为