Question

13．（1）如图（1），在四边形ABCD中，AB∥CD，如果延长DC到点E，使CE=AB，连接AE，那么有S_{四边形ABCD=}S_△ADE，作DE边中点P，连接AP，则AP所在直线为四边形ABCD的面积等分线，你能说明理由吗？
（2）如图（2），如果四边形ABCD中，AB与CD不平行，且S_△ADC＞S_△ABC，过点A能否作出四边形ABCD的面积等分线？若能，请画出面积等分线，并简单说明作图过程．

Answer 1

分析 （1）根据BE∥AC得S_△ACE=S_△ACB，所以S_△AED=S_梯形ABCD，再根据中线性质即可解决．
（2）证明类似（1）．

解答 解：（1）如图1中，∵AB∥EC，AB=EC，
∴四边形ABEC是平行四边形，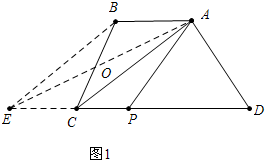
∴BE∥AC，
∴S_△ACE=S_△ACB，
∵S_梯形ABCD=S_△ACB+S_△ACD，S_△AED=S_△ACE+S_△ACD，
∴S_△AED=S_梯形ABCD，
∴S_△AED=S_梯形ABCD，
∵S_梯形ABCD=S_△ACB+S_△ACD，S_△AED=S_△ACE+S_△ACD，
∴S_△AED=S_梯形ABCD，
∵PE=PD，
∴S_△APD=$\frac{1}{2}$S_△AED=$\frac{1}{2}$S_梯形ABCD，
∴直线AP平分梯形ABCD的面积．
（2）如图2中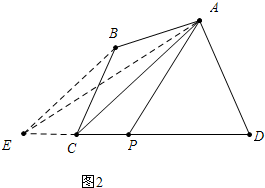，作BE∥AC交DC的延长线于E，连接AE，取DE中点，直线AP就是所求，理由如下：
∵BE∥AC，
∴S_△ACE=S_△ACB，
∵S_梯形ABCD=S_△ACB+S_△ACD，S_△AED=S_△ACE+S_△ACD，
∴S_△AED=S_梯形ABCD，
∵PE=PD，
∴S_△APD=$\frac{1}{2}$S_△AED=${\frac{1}{2}S}_{梯形ABCD}$．

点评 本题考查四边形的面积、三角形的中线的性质、以及同底等高的两个三角形面积等知识，把梯形面积转化为三角形面积是解题的关键．