题目内容
某电脑公司经销甲种型号电脑,受经济危机的影响,电脑价格不断下降,今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定在经销乙种型号电脑,已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
(3)如果乙种电脑每台售价3800元,则(2)中的哪种进货方案使这15台电脑全部售出后获利最多?写出具体进货方案,并求出最多获利是多少?
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定在经销乙种型号电脑,已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
(3)如果乙种电脑每台售价3800元,则(2)中的哪种进货方案使这15台电脑全部售出后获利最多?写出具体进货方案,并求出最多获利是多少?
考点:一次函数的应用,一元一次方程的应用,一元一次不等式组的应用
专题:
分析:(1)根据销售的数量相等,则每台降低的价格乘以台数就是销售额减少的数量,即可列方程求解;
(2)根据销售额的范围即可列不等式组求得电脑台数的范围;
(3)把获利y表示成台数x之间的函数,根据函数的性质求解.
(2)根据销售额的范围即可列不等式组求得电脑台数的范围;
(3)把获利y表示成台数x之间的函数,根据函数的性质求解.
解答:解:(1)设今年三月份M品牌电脑的每台售价是x元.
依题意可得:100000 x+1000=80000 x,
解得x=4000,
经检验x=4000是原方程的解.
答:今年三月份M品牌电脑的每台售价是4000元.
(2)设购进甲种电脑x台,
48000≤3500x+3000(x-15)≤50000,
解得6≤x≤10,
因为的正整数解为6,7,8,9,10,
所以共有5种进货方案;
(3)设总获利为y元,
y=(4000-3500)x+(3800-3000-a)(15-x)=(a-300)x+12000-15a,
当a=300时,(2)中所有方案获利相同.
依题意可得:100000 x+1000=80000 x,
解得x=4000,
经检验x=4000是原方程的解.
答:今年三月份M品牌电脑的每台售价是4000元.
(2)设购进甲种电脑x台,
48000≤3500x+3000(x-15)≤50000,
解得6≤x≤10,
因为的正整数解为6,7,8,9,10,
所以共有5种进货方案;
(3)设总获利为y元,
y=(4000-3500)x+(3800-3000-a)(15-x)=(a-300)x+12000-15a,
当a=300时,(2)中所有方案获利相同.
点评:本题考查了一次函数的应用,求最值的问题常用的方法是转化为函数问题,利用函数的性质求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
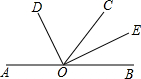 如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.
如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.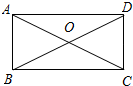 如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠AOD=120°,AB+AC=9,求对角线BD的长及矩形ABCD的面积.
如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠AOD=120°,AB+AC=9,求对角线BD的长及矩形ABCD的面积. 如图,在△ABC中有矩形DGFE,点G,F在BC上,点D,E分别在AB,AC上,AH⊥BC交DE于点M.若DG:DE=2:3,BC=15cm,AH=10cm,求矩形DGFE各边的长.
如图,在△ABC中有矩形DGFE,点G,F在BC上,点D,E分别在AB,AC上,AH⊥BC交DE于点M.若DG:DE=2:3,BC=15cm,AH=10cm,求矩形DGFE各边的长. 如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.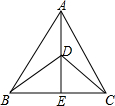 已知,如图,在△ABC中,BD=DC,∠ADB=∠ADC.求证:∠ABC=∠ACB.
已知,如图,在△ABC中,BD=DC,∠ADB=∠ADC.求证:∠ABC=∠ACB.