题目内容
12.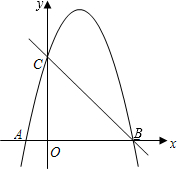 如图,已知抛物线y=ax2+bx-5a经过点(-1,0),C(0,5)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx-5a经过点(-1,0),C(0,5)两点,与x轴交于另一点B.(1)求抛物线的解析式;
(2)若点D(m,m+1)在第一象限的抛物线上,且点D关于直线BC对称的点为E,求点E的坐标;
(3)在(2)的条件下,已知动点P在第一象限点C与点D之间的抛物线上,当△PDE的面积最大时,请求出△PDE的最大面积及此时点P的坐标.
分析 (1)把A(-1,0),C(0,5)代入y=ax2+bx-5a得a$\left\{\begin{array}{l}{a-b-5a=0}\\{-5a=5}\end{array}\right.$,解方程组即可.
(2)先求出点D坐标,求出直线BC的解析式,求出与直线BC垂直的直线的解析式,求出两直线交点的坐标,再利用中点坐标公式,求出点E坐标.
(3)如图,作PM∥y轴交DE于M,设P(m,-m2+4m+5),由(2)可知直线DE的解析式为y=x+1,可得M(m,m+1),根据S△PDE=S△PEM+S△PDM构建二次函数,利用二次函数的性质即可解决问题.
解答 解:(1)把A(-1,0),C(0,5)代入y=ax2+bx-5a得a$\left\{\begin{array}{l}{a-b-5a=0}\\{-5a=5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=4}\end{array}\right.$,
∴抛物线的解析式为y=-x2+4x+5.
(2)∵点D(m,m+1)在第一象限的抛物线上,
∴m+1=-m2+4m+5,
∴m2-3m-4=0,
∴m=4或-1(舍弃),
∴点D坐标(4,5),
对于抛物线y=-x2+4x+5,令y=0,-x2+4x+5=0,解得x=4或-1,
∴B(5,0),∵C(0,5),
∴直线BC的解析式为y=-x+5,
∴过点D与BC垂直的直线的解析式为y=x+1,
由$\left\{\begin{array}{l}{y=x+1}\\{y=-x+5}\end{array}\right.$解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,
∴直线y=x+1与y=-x+5的交点为(2,3),
∵D、E关于点(2,3)对称,
∴点E坐标为(0,1).
(3)如图,作PM∥y轴交DE于M,设P(m,-m2+4m+5),
由(2)可知直线DE的解析式为y=x+1,
∴M(m,m+1),
∴S△PDE=S△PEM+S△PDM=$\frac{1}{2}$•PM•4=2PM=2(-m2+4m+5-m-1)=-2(m-$\frac{3}{2}$)2+$\frac{25}{2}$,
∵-2<0,
∴m=$\frac{3}{2}$时,△PDE的面积有最大值,最大值为$\frac{25}{2}$,此时P($\frac{3}{2}$,$\frac{35}{4}$).
点评 本题考查二次函数综合题、待定系数法、一次函数的应用、三角形的面积等知识,解题的关键是学会利用方程组确定利用函数的交点坐标,学会构建二次函数,解决最值问题,属于中考压轴题.

| A. | 4 | B. | 6 | C. | 5 | D. | 无数 |
| A. | 画一个三角形其内角和为361° | |
| B. | 任意做一个矩形,其对角线相等 | |
| C. | 任取一个实数,其相反数之和为0 | |
| D. | 外观相同的10件同种产品中有2件是不合格产品,现从中抽取一件恰为合格品 |
| A. | $\overrightarrow a$的模为3 | B. | $\overrightarrow a$与$\overrightarrow b$的模之比为-3:1 | ||
| C. | $\overrightarrow a$与$\overrightarrow b$平行且方向相同 | D. | $\overrightarrow a$与$\overrightarrow b$平行且方向相反 |
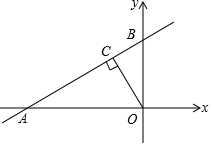 如图,直线y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$与x轴、y轴分别交于A,B两点,过点O作OC⊥AB于点C,点P是OA上的动点,若使△PAC为等腰三角形,则点P的坐标是(2$\sqrt{3}$-4,0)或(-2,0).
如图,直线y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$与x轴、y轴分别交于A,B两点,过点O作OC⊥AB于点C,点P是OA上的动点,若使△PAC为等腰三角形,则点P的坐标是(2$\sqrt{3}$-4,0)或(-2,0).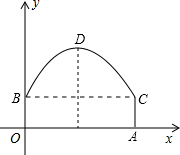 如图,隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,建立直角坐标系,抛物线可用y=-$\frac{1}{6}$x2+bx+c表示.
如图,隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,建立直角坐标系,抛物线可用y=-$\frac{1}{6}$x2+bx+c表示.