题目内容
已知抛物线y=x2-(2m-1)x+m2-m.
(1)求证:此抛物线与x轴必有两个不同的交点;
(2)若此抛物线与直线y=x-3m+3的一个交点在y轴上,求m的值.
(1)求证:此抛物线与x轴必有两个不同的交点;
(2)若此抛物线与直线y=x-3m+3的一个交点在y轴上,求m的值.
考点:抛物线与x轴的交点
专题:
分析:(1)根据二次函数的交点与图象的关系,证明其方程有两个不同的根即△>0即可;
(2)根据题意,令x=0,整理方程可得关于m的方程,解可得m的值.
(2)根据题意,令x=0,整理方程可得关于m的方程,解可得m的值.
解答:(1)证明:令y=0得:x2-(2m-1)x+m2-m=0,
∵△=(2m-1)2-4(m2-m)×1>0,
∴方程有两个不等的实数根,
∴原抛物线与x轴有两个不同的交点;
(2)解:令x=0,根据题意有:m2-m=-3m+3,
解得m=-3或1.
∵△=(2m-1)2-4(m2-m)×1>0,
∴方程有两个不等的实数根,
∴原抛物线与x轴有两个不同的交点;
(2)解:令x=0,根据题意有:m2-m=-3m+3,
解得m=-3或1.
点评:本题是二次函数的综合题,考查二次函数和一元二次方程的关系,二次函数的图象与解析式的关系,抛物线与x轴的交点等.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知B是线段AC上一点,且AB>BC,E是AC中点,F是BC中点,若BC=5,EF+AC=15,则AB=( )
| A、15 | ||
B、
| ||
| C、7 | ||
| D、10 |
 已知,如图,点C、D在⊙O上,直径AB=6cm,弦AC、BD相交于点E.若CE=BC,则阴影部分面积为( )
已知,如图,点C、D在⊙O上,直径AB=6cm,弦AC、BD相交于点E.若CE=BC,则阴影部分面积为( )A、π-
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,已知菱形ABCD的对角线AC、BD的长分别为10cm,24cm,AE⊥BC于点E,则AE的长是
如图,已知菱形ABCD的对角线AC、BD的长分别为10cm,24cm,AE⊥BC于点E,则AE的长是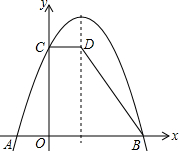 已知:如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.
已知:如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.