题目内容
 已知,如图,点C、D在⊙O上,直径AB=6cm,弦AC、BD相交于点E.若CE=BC,则阴影部分面积为( )
已知,如图,点C、D在⊙O上,直径AB=6cm,弦AC、BD相交于点E.若CE=BC,则阴影部分面积为( )A、π-
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:扇形面积的计算
专题:
分析:连接OD、OC,根据CE=BC,得出∠DBC=∠CEB,进而得出∠DBC=∠A+∠ABD,从而求得
+
=
,得出∠DOC=90°,根据S阴影=S扇形-S△ODC即可求得.
 |
| AD |
 |
| BC |
 |
| DC |
解答: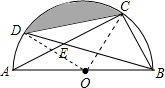 解:连接OD、OC,
解:连接OD、OC,
∵CE=BC,
∴∠DBC=∠CEB,
∵∠CEB=∠A+∠ABD,
∴∠DBC=∠A+∠ABD,
∴
+
=
,
∴
的度数为90°,
∴∠DOC=90°,
∴S阴影=S扇形-S△ODC=
-
×3×3=
-
.
故选B.
 解:连接OD、OC,
解:连接OD、OC,∵CE=BC,
∴∠DBC=∠CEB,
∵∠CEB=∠A+∠ABD,
∴∠DBC=∠A+∠ABD,
∴
 |
| AD |
 |
| BC |
 |
| DC |
∴
 |
| DC |
∴∠DOC=90°,
∴S阴影=S扇形-S△ODC=
| 90π×32 |
| 360 |
| 1 |
| 2 |
| 9π |
| 4 |
| 9 |
| 2 |
故选B.
点评:本题考查了等腰三角形的性质,圆周角和弧之间的关系,扇形的面积等,有一定的难点,求得∠DOC=90°是本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,M,N是线段AB上的两点,且N是线段AM的中点,若AB=14cm,BM=6cm,则AN的长为( )
如图,M,N是线段AB上的两点,且N是线段AM的中点,若AB=14cm,BM=6cm,则AN的长为( )| A、3cm | B、4cm |
| C、6cm | D、7cm |
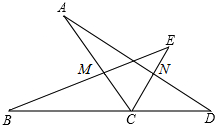 如图,点B,C,D在同一条直线上,∠ACB=∠ECD=60°,∠E=∠D=40°,EC=DC.连结BE,AD,分别交AC,CE于点M,N,下列结论中,错误的是( )
如图,点B,C,D在同一条直线上,∠ACB=∠ECD=60°,∠E=∠D=40°,EC=DC.连结BE,AD,分别交AC,CE于点M,N,下列结论中,错误的是( )| A、∠A=∠B |
| B、△CME≌△CND |
| C、CM=CN |
| D、∠BMC=∠DNC |
 实数a,b在数轴上对应的点如图所示,则下列式子中正确的是( )
实数a,b在数轴上对应的点如图所示,则下列式子中正确的是( )| A、-b+1<0 |
| B、|a-1|=|b+1| |
| C、-b-a>0 |
| D、2a+1>0 |
已知k,n均为非负实数,且2k+n=2,则代数式2k2-4n的最小值为( )
| A、-40 | B、-16 | C、-8 | D、0 |
下列一元二次方程中,无实数根的方程是( )
| A、x2+2x+1=0 |
| B、x2-x+1=0 |
| C、x2-3x+2=0 |
| D、x2+3x-1=0 |