题目内容
 如图,已知菱形ABCD的对角线AC、BD的长分别为10cm,24cm,AE⊥BC于点E,则AE的长是
如图,已知菱形ABCD的对角线AC、BD的长分别为10cm,24cm,AE⊥BC于点E,则AE的长是考点:菱形的性质
专题:
分析:利用菱形的性质以及勾股定理得出其边长,进而利用菱形的面积求法得出即可.
解答:解:∵四边形ABCD是菱形,
∴AO=CO,BO=DO,AC⊥BD,
∵对角线AC、BD的长分别为10cm,24cm,
∴AO=CO=5cm,BO=DO=12cm,
∴BC=CD=AB=AD=13cm,
∴
AC×BD=BC×AE,
故AE=
=
(cm).
故答案为:
.
∴AO=CO,BO=DO,AC⊥BD,
∵对角线AC、BD的长分别为10cm,24cm,
∴AO=CO=5cm,BO=DO=12cm,
∴BC=CD=AB=AD=13cm,
∴
| 1 |
| 2 |
故AE=
| ||
| 13 |
| 120 |
| 13 |
故答案为:
| 120 |
| 13 |
点评:此题主要考查了菱形的性质以及勾股定理等知识,得出菱形的边长是解题关键.

练习册系列答案
相关题目
若x+y=2,xy=-2,则
+
的值是( )
| y |
| x |
| x |
| y |
| A、2 | B、-2 | C、4 | D、-4 |
 如图,M,N是线段AB上的两点,且N是线段AM的中点,若AB=14cm,BM=6cm,则AN的长为( )
如图,M,N是线段AB上的两点,且N是线段AM的中点,若AB=14cm,BM=6cm,则AN的长为( )| A、3cm | B、4cm |
| C、6cm | D、7cm |
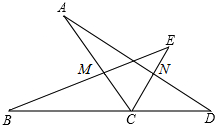 如图,点B,C,D在同一条直线上,∠ACB=∠ECD=60°,∠E=∠D=40°,EC=DC.连结BE,AD,分别交AC,CE于点M,N,下列结论中,错误的是( )
如图,点B,C,D在同一条直线上,∠ACB=∠ECD=60°,∠E=∠D=40°,EC=DC.连结BE,AD,分别交AC,CE于点M,N,下列结论中,错误的是( )| A、∠A=∠B |
| B、△CME≌△CND |
| C、CM=CN |
| D、∠BMC=∠DNC |
 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.