Question

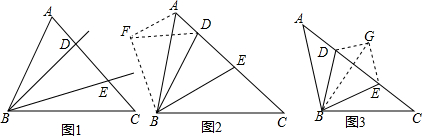
如图，在△ABC中，BA=BC，∠ABC=90°∠DBE是以点B为顶点的角，且∠DBE在∠ABC内绕点B转动，BD、BE分别交AC于点D、E，若∠DBE=45°，请说明无论∠DBE旋转到什么位置，始终满足：DE²=AD²+EC²．

Answer 1

考点：旋转的性质,勾股定理,勾股定理的逆定理

专题：

分析：根据等腰三角形的性质得∠C=∠1=45°，再把△BCE绕点B逆时针旋转90°可得到△BAF，根据旋转的性质得∠2=∠C=45°，∠ABF=∠CBE，∠FBE=90°，AF=CE，BF=BE，由于∠DBE=45°，则∠DBF=45°，则可根据“SAS”判断△DBF≌△DBE得到DF=DE，接着证明△AFD为直角三角形，然后利用勾股定理得到DF²=AD²+AF²，再利用等线段代换即可得到DE²=AD²+EC²．

解答：证明：∵BA=BC，∠ABC=90°，
∴∠C=∠1=45°，
∴把△BCE绕点B逆时针旋转90°可得到△BAF，
∴∠2=∠C=45°，∠ABF=∠CBE，∠FBE=90°，AF=CE，BF=BE，
∵∠DBE=45°，
∴∠DBF=45°，
∴∠DBF=∠DBE，
在△DBF和△DBE中，

BD=BD ∠DBF=∠DBE BF=BE

，
∴△DBF≌△DBE（SAS），
∴DF=DE，
∵∠1+∠2=90°，
∴△AFD为直角三角形，
∴DF²=AD²+AF²，
∴DE²=AD²+EC²．
即无论∠DBE旋转到什么位置，始终满足：DE²=AD²+EC²．

点评：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了勾股定理．