题目内容
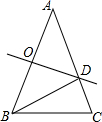 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,则下列结论:①BD平分∠ABC;②AD=BD=BC;③△BCD的周长等于AB+BC;④∠C=2∠A;⑤S△BCD=S△ABD,正确的个数( )
如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,则下列结论:①BD平分∠ABC;②AD=BD=BC;③△BCD的周长等于AB+BC;④∠C=2∠A;⑤S△BCD=S△ABD,正确的个数( )| A、2个 | B、3个 | C、4个 | D、5个 |
考点:线段垂直平分线的性质,等腰三角形的性质
专题:
分析:由在△ABC中,AB=AC,∠A=36°,可求得∠ABC与∠C的度数,又由AB的垂直平分线OD交AB于点O,交AC于点D,即可求得①BD平分∠ABC;继而证得△BCD是等腰三角形,则可得②AD=BD=BC,则可求得③△BCD的周长等于AB+B;④∠C=2∠AC;又由AD=BD>CD,可得S△BCD<S△ABD.
解答:解:①∵在△ABC中,AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵AB的垂直平分线OD交AB于点O,交AC于点D,
∴AD=BD,
∴∠ABD=∠A=36°,
∴∠CBD=∠ABC-∠ABD=36°,
∴∠ABD=∠CBD=36°,
即BD平分∠ABC,故①正确;
②∴∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴AD=BD=BC,故②正确;
③∴△BCD的周长为:BC+CD+BD=BC+CD+AD=BC+AC=AB+BC;故③正确;
④∵∠C=72°,∠A=36°,
∴∠C=2∠A,故④正确;
⑤∵AD=BD>CD,
∴S△BCD<S△ABD,故⑤错误.
故选C.
∴∠ABC=∠C=72°,
∵AB的垂直平分线OD交AB于点O,交AC于点D,
∴AD=BD,
∴∠ABD=∠A=36°,
∴∠CBD=∠ABC-∠ABD=36°,
∴∠ABD=∠CBD=36°,
即BD平分∠ABC,故①正确;
②∴∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴AD=BD=BC,故②正确;
③∴△BCD的周长为:BC+CD+BD=BC+CD+AD=BC+AC=AB+BC;故③正确;
④∵∠C=72°,∠A=36°,
∴∠C=2∠A,故④正确;
⑤∵AD=BD>CD,
∴S△BCD<S△ABD,故⑤错误.
故选C.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
下列是计算正确的是( )
| A、-8-3=-5 |
| B、-(-2)2=4 |
| C、-(x-y)=x+y |
| D、ab+2ba=3ab |
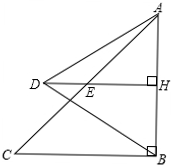 已知,如图:△ABC是等腰直角三角形,∠ABC=90°,D为△ABC外一点,连接AD、BD,过点D作DH⊥AB,垂足为H,交AC于E,已知AD=BD=2.
已知,如图:△ABC是等腰直角三角形,∠ABC=90°,D为△ABC外一点,连接AD、BD,过点D作DH⊥AB,垂足为H,交AC于E,已知AD=BD=2. 如图,某中学为方便师生活动,准备在长30m、宽20m的矩形草坪上修筑两横两纵四条小路,横、纵路的宽度之比为3:2,若要使余下的草坪面积是原来草坪面积的
如图,某中学为方便师生活动,准备在长30m、宽20m的矩形草坪上修筑两横两纵四条小路,横、纵路的宽度之比为3:2,若要使余下的草坪面积是原来草坪面积的