题目内容
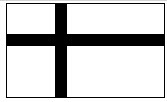 如图,某中学为方便师生活动,准备在长30m、宽20m的矩形草坪上修筑两横两纵四条小路,横、纵路的宽度之比为3:2,若要使余下的草坪面积是原来草坪面积的
如图,某中学为方便师生活动,准备在长30m、宽20m的矩形草坪上修筑两横两纵四条小路,横、纵路的宽度之比为3:2,若要使余下的草坪面积是原来草坪面积的| 3 |
| 4 |
考点:一元二次方程的应用
专题:几何图形问题
分析:设平均每份为x米,则横路的宽为3x米,纵路的宽为2x米,根据余下的草坪面积是原来草坪面积的
建立方程求出其解即可.
| 3 |
| 4 |
解答:解:设平均每份为x米,则横路的宽为3x米,纵路的宽为2x米,由题意,得
(30-4x)(20-6x)=30×20×
,
解得:x1=65+5
(舍去),x2=65-5
.
故横路的宽为:(195-15
)米,纵路的宽为(130-10
)米.
答:横路的宽为:(195-15
)米,纵路的宽为(130-10
)米.

(30-4x)(20-6x)=30×20×
| 3 |
| 4 |
解得:x1=65+5
| 103 |
| 103 |
故横路的宽为:(195-15
| 103 |
| 103 |
答:横路的宽为:(195-15
| 103 |
| 103 |
点评:本题考查了矩形的面积公式的运用,列一元二次方程解实际问题的运用,一元二次方程的解法的运用,解答时根据余下的草坪面积是原来草坪面积的
建立方程是关键.
| 3 |
| 4 |

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
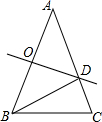 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,则下列结论:①BD平分∠ABC;②AD=BD=BC;③△BCD的周长等于AB+BC;④∠C=2∠A;⑤S△BCD=S△ABD,正确的个数( )
如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,则下列结论:①BD平分∠ABC;②AD=BD=BC;③△BCD的周长等于AB+BC;④∠C=2∠A;⑤S△BCD=S△ABD,正确的个数( )| A、2个 | B、3个 | C、4个 | D、5个 |
直径为8的圆内有一点M到圆心O的距离是3,则过点M的弦中,长度为整数的条数为( )
| A、3 | B、4 | C、5 | D、6 |
 如图,AB是半圆的直径,直线MN切半圆于C,同AM⊥MN,BN⊥MN,如果AM=6,BN=8,那么半圆的直径是
如图,AB是半圆的直径,直线MN切半圆于C,同AM⊥MN,BN⊥MN,如果AM=6,BN=8,那么半圆的直径是