题目内容
3.若$\left\{\begin{array}{l}{x+y=6}\\{xy=7}\end{array}\right.$,则x3+y3=90.分析 根据代入消元法,可得关于x的一元二次方程,可得方程组的解,根据代数式求值,可得答案.
解答 解:由x+y=6,得y=6-x①,
将①代入xy=7,得
x(6-x)=7,
解得x=3+$\sqrt{2}$,y=3-$\sqrt{2}$,
x=3-$\sqrt{2}$,y=3+$\sqrt{2}$.
x3+y3=(3+$\sqrt{2}$)3+(3-$\sqrt{2}$)3=90,
故答案为:90.
点评 本题考查了解二元一次方程组,利用代入消元法得出方程组的解是解题关键.

练习册系列答案
相关题目
3. 如图,在下列说法中错误的是( )
如图,在下列说法中错误的是( )
 如图,在下列说法中错误的是( )
如图,在下列说法中错误的是( )| A. | 射线OA的方向是正西方向 | B. | 射线OB的方向是西南方向 | ||
| C. | 射线OC的方向是南偏东60° | D. | 射线OD的方向是北偏东55° |
4.下列四个整式:①x2-4x+4; ②6x2+3x+1; ③4x2+4x+1; ④x2+4xy+2y2.其中是完全平方式的是( )
| A. | ①③ | B. | ①②③ | C. | ②③④ | D. | ③④ |
1.若关于x的方程ax+3x=2的解与方程2x+1=3的解相同,则a的值是( )
| A. | 1 | B. | 5 | C. | -1 | D. | -5 |
8.Rt△ABC中,斜边BC上的中线AD=5,则AB2+AC2的值为( )
| A. | 169 | B. | 100 | C. | 25 | D. | 13 |
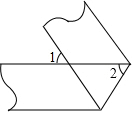 如图将一条两边都互相平行的纸带进行折叠,设∠1为α度,则∠2=90°-$\frac{1}{2}$α.(请用含有α的代数式表示)
如图将一条两边都互相平行的纸带进行折叠,设∠1为α度,则∠2=90°-$\frac{1}{2}$α.(请用含有α的代数式表示)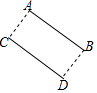 如图所示,平移线段AB到CD的位置,则AB=CD,CD∥AB,BD=AC.
如图所示,平移线段AB到CD的位置,则AB=CD,CD∥AB,BD=AC.