题目内容
13.在Rt△ABC中,∠C=90°,AC=4,BC=6,求AB边上的高.分析 如图所示,CD即为AB边上的高,在直角三角形ABC中,利用勾股定理求出AB的长,再利用面积法求出CD的长即可.
解答  解:如图所示,CD即为AB边上的高,
解:如图所示,CD即为AB边上的高,
在Rt△ABC中,∠C=90°,AC=4,BC=6,
根据勾股定理得:AB=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,
∵CD⊥AB,
∴S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$BC•AC,即AB•CD=BC•AC,
∴CD=$\frac{4×6}{2\sqrt{13}}$=$\frac{12\sqrt{13}}{13}$.
点评 此题考查了勾股定理,以及三角形的面积,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
12.下列各式表示正确的是( )
| A. | $\sqrt{9}$=±3 | B. | ±$\sqrt{9}$=3 | C. | $±\sqrt{9}$=±3 | D. | ±$\sqrt{(-3)^{2}}$=-3 |
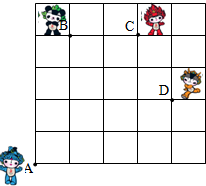 如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中 如图是一组密码的一部分,为了保密,许多情况下可采用不同的密码,请你运用所学数学知识找到破译密码的“钥匙”,目前,已破译处“正做数学”的真实意义是“”祝你成功,若“正”所处的位置为(x,y),你找到的密码钥匙是(x-1,y-2),破译的“今天考试”真实意思是努力发挥.
如图是一组密码的一部分,为了保密,许多情况下可采用不同的密码,请你运用所学数学知识找到破译密码的“钥匙”,目前,已破译处“正做数学”的真实意义是“”祝你成功,若“正”所处的位置为(x,y),你找到的密码钥匙是(x-1,y-2),破译的“今天考试”真实意思是努力发挥.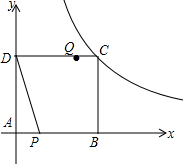 已知正方形ABCD,顶点A与坐标原点重合,顶点B、D分别在x轴和y轴的正半轴上,顶点C在反比例函数y=$\frac{16}{x}$(x>0)的图象上,如图所示,动点P以每秒1个单位的速度从A点出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC-CB-BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.
已知正方形ABCD,顶点A与坐标原点重合,顶点B、D分别在x轴和y轴的正半轴上,顶点C在反比例函数y=$\frac{16}{x}$(x>0)的图象上,如图所示,动点P以每秒1个单位的速度从A点出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC-CB-BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.