题目内容
2.代数基本定理告诉我们对于形如xn+${a}_{1}{x}^{n-1}$$+{a}_{2}{x}^{n-2}$+…+an-1x+an=0(其中a1,a2,…an为整数)这样的方程,如果有整数根的话,那么整数根必定是an的约数.例如方程x3+8x2-11x+2=0的整数根只可能为±1,±2代入检验得x=1时等式成立.故x3+8x2-11x+2含有因式x-1,所以原方程可转化为:(x-1)(x2+9x-2)=0,进而可求得方程的所有解.根据以上阅读材料请你解方程:x3+x2-11x-3=0.分析 把x=±1,±3代入方程进行验证得到x=3符合题意,故x3+x2-11x-3=0含有因式(x-3),由此进行因式分解即可
解答 解:取x=±1,±3代入方程,得x=3适合方程,则
原方程可以分解为:(x-3)(x3+4x+1)=0,
解得x=3或x=-2+$\sqrt{3}$.
点评 本题考查了因式分解的意义.因式分解是恒等变形,因此可以用整式乘法来检验.

练习册系列答案
相关题目
14.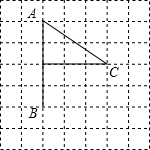 如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )
如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )
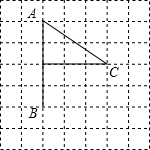 如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )
如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )| A. | (2,3) | B. | (1,3) | C. | (3,1) | D. | (3,0) |
12.若a3xby与-2a2ybx+1是同类项,则x+y=( )
| A. | 1 | B. | -1 | C. | -5 | D. | 5 |
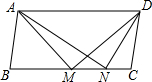 如图,平行四边形ABCD中,M、N是BC边上的点,且∠AMD=∠AND=90°,则下列结论中一定成立的是(1)(3)(4)(把所有正确结论的序号都填在横线上)
如图,平行四边形ABCD中,M、N是BC边上的点,且∠AMD=∠AND=90°,则下列结论中一定成立的是(1)(3)(4)(把所有正确结论的序号都填在横线上)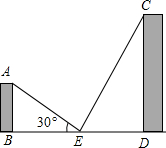 如图,两座建筑物AB与CD,其地面距离BD为60米,E为BD的中点,从E点测得A的仰角为30°,从C处测得E的俯角为60°,现准备在点A与点C之间拉一条绳子挂上小彩旗(不计绳子弯曲),求绳子AC的长度.(结果保留一位小数,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,两座建筑物AB与CD,其地面距离BD为60米,E为BD的中点,从E点测得A的仰角为30°,从C处测得E的俯角为60°,现准备在点A与点C之间拉一条绳子挂上小彩旗(不计绳子弯曲),求绳子AC的长度.(结果保留一位小数,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)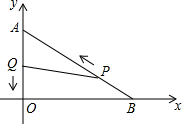 如图,在平面直角坐标系中,已知OA=6厘米,OB=8厘米.点P从点B开始沿BA边向终点A以1厘米/秒的速度移动;点Q从点A开始沿AO边向终点O以1厘米/秒的速度移动.若P、Q同时出发,运动时间为t(s).
如图,在平面直角坐标系中,已知OA=6厘米,OB=8厘米.点P从点B开始沿BA边向终点A以1厘米/秒的速度移动;点Q从点A开始沿AO边向终点O以1厘米/秒的速度移动.若P、Q同时出发,运动时间为t(s).