题目内容
如图1,均匀的向一个由三个等高圆柱组合成的容器中注水(圆柱底面半径从小到大分别为acm,bcm,ccm),最后把圆柱注满,水面高度h(cm)随时间t(s)的变化规律如图2所示.
(1)这个容器的性状是图1中 ,容器深度为 cm;
(2)若a=5cm,求注水速度v(单位:cm3/s)及b,c的值(π取3);
(3)求注水全过程中容器的水深h(cm)与注水时间t(s)的函数解析式;
(4)画出图中向另两个容器注水时水面高度h随时间t变化的图象(不用列表).

(1)这个容器的性状是图1中
(2)若a=5cm,求注水速度v(单位:cm3/s)及b,c的值(π取3);
(3)求注水全过程中容器的水深h(cm)与注水时间t(s)的函数解析式;
(4)画出图中向另两个容器注水时水面高度h随时间t变化的图象(不用列表).

考点:一次函数的应用
专题:
分析:(1)由函数图象就可以得出函数图象表示的是容器③,容器的深度为30cm;
(2)先求出最小圆柱的体积,就可以求出注水速度,根据注水速度就可以都分别求出b、c的值;
(3)由求分段函数的方法当0≤t≤100,100<t≤325,325<t≤350时由待定系数法就可以求出结论;
(4)根据图2的数据就可以直接画出①、②的函数图象.
(2)先求出最小圆柱的体积,就可以求出注水速度,根据注水速度就可以都分别求出b、c的值;
(3)由求分段函数的方法当0≤t≤100,100<t≤325,325<t≤350时由待定系数法就可以求出结论;
(4)根据图2的数据就可以直接画出①、②的函数图象.
解答:解:(1)由函数可以直接得出:
这个容器的性状是图1中③,容器深度为30cm.
故答案为:③,30;
(2)由题意,得
小圆柱的体积为:π×25×30=750πcm3,
注水速度为:v=750π÷(350-325)=30πcm3/s.
较小圆柱的体积为:30π×100=3000πcm3,
最大圆柱的体积为:30π×125=3750πcm3,
∴b=
=10
cm,
c=
=5
cm.
答:注水速度v=30πcm3/s,b=10
cm,c=5
cm;
(3)当0≤t≤100时,设h与t之间的函数关系式为h1=k1t,由题意,得
10=100k1,
解得:k1=0.1,
h1=0.1t;
当100<t≤325时,设h与t之间的函数关系式为h2=k2t+b2,由题意,得
,
解得:
,
h2=
t+2,;
当325<t≤350时,设h与t之间的函数关系式为h3=k3t+b3,由题意,得
,
解得:
,
h3=0.4t-110.
综上所述,h=
;
(4)由题意,根据图2折线关系就可以得出:
①的图象
 ,
,
②的图象

这个容器的性状是图1中③,容器深度为30cm.
故答案为:③,30;
(2)由题意,得
小圆柱的体积为:π×25×30=750πcm3,
注水速度为:v=750π÷(350-325)=30πcm3/s.
较小圆柱的体积为:30π×100=3000πcm3,
最大圆柱的体积为:30π×125=3750πcm3,
∴b=
|
| 3 |
c=
|
| 15 |
答:注水速度v=30πcm3/s,b=10
| 3 |
| 15 |
(3)当0≤t≤100时,设h与t之间的函数关系式为h1=k1t,由题意,得
10=100k1,
解得:k1=0.1,
h1=0.1t;
当100<t≤325时,设h与t之间的函数关系式为h2=k2t+b2,由题意,得
|
解得:
|
h2=
| 2 |
| 25 |
当325<t≤350时,设h与t之间的函数关系式为h3=k3t+b3,由题意,得
|
解得:
|
h3=0.4t-110.
综上所述,h=
|
(4)由题意,根据图2折线关系就可以得出:
①的图象
 ,
,②的图象

点评:本题考查了圆柱的体积公式的运用,分段函数的运用,待定系数法求一次函数的解析式的运用,解答时结合图形和函数图象,弄清函数图象的数据含义是关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 已知菱形ABCD中,点R是CD上的一个动点,过A,R的直线交BD于O,交BC的延长线于S.
已知菱形ABCD中,点R是CD上的一个动点,过A,R的直线交BD于O,交BC的延长线于S. 如图,分别以等腰Rt△ACD的边AD、AC、CD为直径画半圆,求证:所得两个月型图案AGCE和DHCF的面积之和(图中阴影部分)等于Rt△ACD的面积.
如图,分别以等腰Rt△ACD的边AD、AC、CD为直径画半圆,求证:所得两个月型图案AGCE和DHCF的面积之和(图中阴影部分)等于Rt△ACD的面积.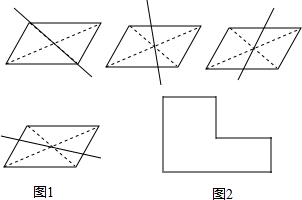 (1)我们知道把平行四边形分成面积相等的两部分的直线有无数条,如图1,这些直线都经过平行四边形的
(1)我们知道把平行四边形分成面积相等的两部分的直线有无数条,如图1,这些直线都经过平行四边形的 如图,某乡村学校有教学楼A,在A楼的南偏西45°方向距A楼300
如图,某乡村学校有教学楼A,在A楼的南偏西45°方向距A楼300