题目内容
15.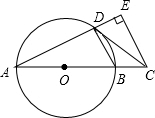 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
分析 (1)连接OD,由CD是⊙O切线,得到∠ODC=90°,根据AB为⊙O的直径,得到∠ADB=90°,等量代换得到∠BDC=∠ADO,根据等腰三角形的性质得到∠ADO=∠A,即可得到结论;
(2)根据垂直的定义得到∠E=∠ADB=90°,根据平行线的性质得到∠DCE=∠BDC,根据相似三角形的性质得到$\frac{CE}{DE}=\frac{AE}{CE}$,解方程即可得到结论.
解答  (1)证明:连接OD,
(1)证明:连接OD,
∵CD是⊙O切线,
∴∠ODC=90°,
即∠ODB+∠BDC=90°,
∵AB为⊙O的直径,
∴∠ADB=90°,
即∠ODB+∠ADO=90°,
∴∠BDC=∠ADO,
∵OA=OD,
∴∠ADO=∠A,
∴∠BDC=∠A;
(2)∵CE⊥AE,
∴∠E=∠ADB=90°,
∴DB∥EC,
∴∠DCE=∠BDC,
∵∠BDC=∠A,
∴∠A=∠DCE,
∵∠E=∠E,
∴△AEC∽△CED,
∴$\frac{CE}{DE}=\frac{AE}{CE}$,
∴EC2=DE•AE,
∴16=2(2+AD),
∴AD=6.
点评 本题考查了切线的性质,相似三角形的判定和性质,平行线的性质,熟练掌握切线的性质是解题的关键.

练习册系列答案
相关题目
3.下列计算结果正确的是( )
| A. | a8÷a4=a2 | B. | a2•a3=a6 | C. | (a3)2=a6 | D. | (-2a2)3=8a6 |
7.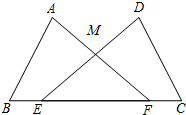 如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
 如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )| A. | ∠B | B. | ∠A | C. | ∠EMF | D. | ∠AFB |
4.二次根式$\sqrt{2-x}$有意义,则x的取值范围是( )
| A. | x>2 | B. | x<2 | C. | x≥2 | D. | x≤2 |
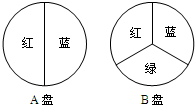 用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?请你并说明理由.
用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?请你并说明理由.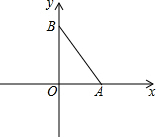 如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为(3,4)或($\frac{96}{25}$,$\frac{72}{25}$)或(-$\frac{21}{25}$,$\frac{28}{25}$).
如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为(3,4)或($\frac{96}{25}$,$\frac{72}{25}$)或(-$\frac{21}{25}$,$\frac{28}{25}$).