题目内容
20.数据499,500,501,500的中位数是500.分析 先将题中的数据按照从小到大的顺序排列,再根据中位数的概念解答即可.
解答 解:将该组数据按照从小到大的顺序排列为:499,500,500,501,
可得改组数据的中位数为:$\frac{500+500}{2}$=500,
故答案为:500.
点评 本题考查了中位数的概念:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
10. 如图,C在以AB为直径的半圆⊙O上,I是△ABC的内心,AI,BI 的延长线分别交半圆⊙O于点D,E,AB=6,则DE的长为( )
如图,C在以AB为直径的半圆⊙O上,I是△ABC的内心,AI,BI 的延长线分别交半圆⊙O于点D,E,AB=6,则DE的长为( )
 如图,C在以AB为直径的半圆⊙O上,I是△ABC的内心,AI,BI 的延长线分别交半圆⊙O于点D,E,AB=6,则DE的长为( )
如图,C在以AB为直径的半圆⊙O上,I是△ABC的内心,AI,BI 的延长线分别交半圆⊙O于点D,E,AB=6,则DE的长为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 5 |
11.函数y=$\sqrt{2-x}$中自变量x的取值范围是( )
| A. | x≤2 | B. | x≥2 | C. | x<2 | D. | x≠2 |
5.下表是博文学校初三•一班慧慧、聪聪两名学生入学以来10次数学检测成绩(单位:分).
回答下列问题:
(1)分别求出慧慧和聪聪成绩的平均数;
(2)分别计算慧慧和聪聪两组数据的方差;
(3)根据(1)(2)你认为选谁参加全国数学竞赛更合适?并说明理由;
(4)由于初三•二班、初三•三班和初三•四班数学成绩相对薄弱,学校打算派慧慧和聪聪分别参加三个班的数学业余辅导活动,求两名学生分别在初三•二班和初三•三班的概率.
| 慧慧 | 116 | 124 | 130 | 126 | 121 | 127 | 126 | 122 | 125 | 123 |
| 聪聪 | 122 | 124 | 125 | 128 | 119 | 120 | 121 | 128 | 114 | 119 |
(1)分别求出慧慧和聪聪成绩的平均数;
(2)分别计算慧慧和聪聪两组数据的方差;
(3)根据(1)(2)你认为选谁参加全国数学竞赛更合适?并说明理由;
(4)由于初三•二班、初三•三班和初三•四班数学成绩相对薄弱,学校打算派慧慧和聪聪分别参加三个班的数学业余辅导活动,求两名学生分别在初三•二班和初三•三班的概率.
17.下面各式中,计算正确的是( )
| A. | 2-3=1 | B. | $3×(-\frac{1}{3})=1$ | C. | $\root{3}{-1}=-1$ | D. | -32=9 |
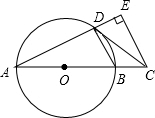 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.