题目内容
12.已知a+b=2,ab=-3,(1)求a2+b2的值;
(2)求$\frac{1}{2}$a3b-a2b2+$\frac{1}{2}$ab3的值.
分析 (1)a2+b2化为(a+b)2-2ab代入计算即可;
(2)提取公因式后用公式因式分解后代入计算即可.
解答 解:(1)∵a+b=2,ab=-3
∴a2+b2=(a+b)2-2ab=22-2×(-3)=4+6=10;
(2)$\frac{1}{2}$a3b-a2b2+$\frac{1}{2}$ab3=$\frac{1}{2}$ab(a2-2ab+b2)=$\frac{1}{2}$ab(a-b)2=$\frac{1}{2}$ab[(a+b)2-4ab]=$\frac{1}{2}×$(-3)×16=-24.
点评 本题考查了因式分解的应用及完全平方公式的知识,解题的关键是牢记因式分解的方法,难度不大.

练习册系列答案
相关题目
3.与-3x2y的乘积是9x6y3的单项式是( )
| A. | -3x4y2 | B. | -3x3y3 | C. | -27x8y4 | D. | 12x3y3 |
20.下列说法中,正确的是( )
| A. | (-3)2是负数 | B. | 若|x|=5,则x=5或-5 | ||
| C. | 最小的有理数是零 | D. | 任何有理数的绝对值都大于零 |
17.下面各式中,计算正确的是( )
| A. | 2-3=1 | B. | $3×(-\frac{1}{3})=1$ | C. | $\root{3}{-1}=-1$ | D. | -32=9 |
4.单项式乘以多项式运算法则的依据是( )
| A. | 乘法交换律 | B. | 加法结合律 | C. | 乘法分配律 | D. | 加法交换律 |
1.a表示两个相邻整数的平均数的平方,b表示这两个相邻整数平方数的平均数,那么a与b的大小关系是( )
| A. | a>b | B. | a≥b | C. | a≤b | D. | a<b |
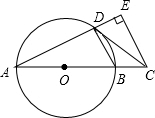 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.