题目内容
2.已知方程2x2-3x-2=0的两个解分别为x1、x2,则x1+x2的值为$\frac{3}{2}$.分析 直接根据根与系数的关系求解.
解答 解:根据题意得x1+x2=-$\frac{-3}{2}$=$\frac{3}{2}$.
故答案为$\frac{3}{2}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列式子中是完全平方式的是( )
| A. | a2+2ab+b2 | B. | a2+2a+2 | C. | a2-2b+b2 | D. | a2+2a+b2 |
17.下列各数中,属于无理数的是( )
| A. | -2 | B. | 0 | C. | $\sqrt{3}$ | D. | 0.101001000 |
11.若不等式组$\left\{\begin{array}{l}{1+x<a}\\{3-x≤0}\end{array}\right.$有解,则实数a的取值范围是( )
| A. | a<4 | B. | a≤4 | C. | a>4 | D. | a≥4 |
12.某射击教练对甲、乙两个射击选手的5次成绩(单位:环)进行了统计,如表
所示:设甲、乙两人射击成绩的平均数分别为$\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,射击成绩的方差分别为${s_甲}^2$、${s_乙}^2$,则下列判断中正确的是( )
| 甲 | 10 | 9 | 8 | 5 | 8 |
| 乙 | 8 | 8 | 7 | 9 | 8 |
| A. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,${s_甲}^2$>${s_乙}^2$ | B. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2$<${s_乙}^2$ | ||
| C. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2={s_乙}^2$ | D. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2$>${s_乙}^2$ |
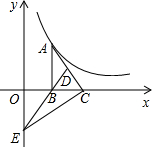 如图,Rt△ABC的直角边BC在x轴正半轴上,点D为斜边AC上一点,AD=2CD,DB的延长线交y轴于点E,函数y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BCE=2,则k=8.
如图,Rt△ABC的直角边BC在x轴正半轴上,点D为斜边AC上一点,AD=2CD,DB的延长线交y轴于点E,函数y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BCE=2,则k=8.