题目内容
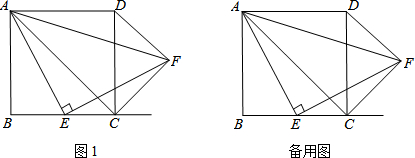
如图,四边形ABCD是正方形,点E是BC的中点,∠AEF=90°,EF交正方形外角的平分线CF于F,连接AC、AF、DF,求证:
(1)AE=EF;
(2)△ABE∽△ACF;
(3)△DFC是等腰直角三角形.
(1)AE=EF;
(2)△ABE∽△ACF;
(3)△DFC是等腰直角三角形.

考点:正方形的性质,全等三角形的判定与性质,相似三角形的判定与性质
专题:
分析:(1)取AB中点M,连接ME,利用正方形的性质和等腰直角三角形的性质,证得△AME≌△ECF,得出结论;
(2)利用(1)图,△AEF是等腰直角三角形,∠2=∠4,∠ACF=∠B,证得结论;
(3)过F作FN⊥BC的延长线于N,证得△FNE≌△EBA,得出△FCN是等腰直角三角形,易证四边形FNCP为矩形(正方形),求得∠FDC=∠DCF得出结论.
(2)利用(1)图,△AEF是等腰直角三角形,∠2=∠4,∠ACF=∠B,证得结论;
(3)过F作FN⊥BC的延长线于N,证得△FNE≌△EBA,得出△FCN是等腰直角三角形,易证四边形FNCP为矩形(正方形),求得∠FDC=∠DCF得出结论.
解答:证明:(1)如图(1),
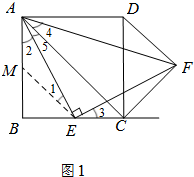
取AB中点M,连接ME,
则AM=BM=BE=CE=
正方形边长,
∴在Rt△BME中,∠BME=∠BEM=45°,
∴∠AME=135°,∠1+∠2=45°.
∵∠AEF=90°,
∴∠1+∠3=45°
∴∠2=∠3.
∵CF是正方形外角的平分线,
∴∠DCF=
×90°=45°,
∴∠ECF=90°+45°=∠AME.
在△AME和△ECF中,
∴△AME≌△ECF(ASA)
∴AE=EF.
(2)如图(1),
∵∠AEF=90°,AE=EF,
∴△AEF是等腰直角三角形,
∴∠EAF=45°,即∠4+∠5=45°.
∵AC为正方形ABCD的对角线,
∴∠BAC=45°,即∠2+∠5=45°,
∴∠2=∠4.
∵∠DCF=∠DCA=
×90°=45°,
∴∠ACF=45°+45°=90°=∠B,
∴△ABE∽△ACF.
(3)(法一)如图(2),
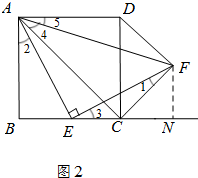
设正方形ABCD边长为2a,则BE=a,AE=EF=
a.
∵△AEF是等腰直角三角形,
∴AF=
AE=
a.
过F作FN⊥BC的延长线于N,
则∠FNE=90°=∠B.
又由(1)知,∠3=∠2,EF=AE,
在△FNE和△EBA中,
,
∴△FNE≌△EBA(AAS),
∴FN=BE=a.
∵△FCN是等腰直角三角形,
∴CF=
FN=
a,
∴
=
=
.
∵∠1+∠3=45°,∠4+∠5=45°,∠3=∠2=∠4,
∴∠5=∠1,
∴易证四边形FNCP为矩形(正方形),
∴∠ADF=∠FCE=135°,
∴∠ADF=∠FCE=135°,
∴∠FDC=45°=∠DCF,
∴△DFC是等腰直角三角形.
(法二)如图(3),过F分别作FN⊥BC的延长线于N,FP⊥CD于P,

则∠FNE=90°=∠B.
由(1)知,∠3=∠2,EF=AE,
在△FNE和△EBA中,
∴△FNE≌△EBA(AAS),
∴FN=BE=
BC=
CD.
易证四边形FNCP为矩形(正方形),
则CP=FN=
CD,
∴FP垂直平分CD,
∴FD=FC.
∵∠DCF=
×90°=45°,
∴∠FDC=∠DCF=45°,
∴△DFC是等腰直角三角形.

取AB中点M,连接ME,
则AM=BM=BE=CE=
| 1 |
| 2 |
∴在Rt△BME中,∠BME=∠BEM=45°,
∴∠AME=135°,∠1+∠2=45°.
∵∠AEF=90°,
∴∠1+∠3=45°
∴∠2=∠3.
∵CF是正方形外角的平分线,
∴∠DCF=
| 1 |
| 2 |
∴∠ECF=90°+45°=∠AME.
在△AME和△ECF中,
|
∴△AME≌△ECF(ASA)
∴AE=EF.
(2)如图(1),
∵∠AEF=90°,AE=EF,
∴△AEF是等腰直角三角形,
∴∠EAF=45°,即∠4+∠5=45°.
∵AC为正方形ABCD的对角线,
∴∠BAC=45°,即∠2+∠5=45°,
∴∠2=∠4.
∵∠DCF=∠DCA=
| 1 |
| 2 |
∴∠ACF=45°+45°=90°=∠B,
∴△ABE∽△ACF.
(3)(法一)如图(2),

设正方形ABCD边长为2a,则BE=a,AE=EF=
| 5 |
∵△AEF是等腰直角三角形,
∴AF=
| 2 |
| 10 |
过F作FN⊥BC的延长线于N,
则∠FNE=90°=∠B.
又由(1)知,∠3=∠2,EF=AE,
在△FNE和△EBA中,
|
∴△FNE≌△EBA(AAS),
∴FN=BE=a.
∵△FCN是等腰直角三角形,
∴CF=
| 2 |
| 2 |
∴
| AF |
| AD |
| EF |
| CF |
| ||
| 2 |
∵∠1+∠3=45°,∠4+∠5=45°,∠3=∠2=∠4,
∴∠5=∠1,
∴易证四边形FNCP为矩形(正方形),
∴∠ADF=∠FCE=135°,
∴∠ADF=∠FCE=135°,
∴∠FDC=45°=∠DCF,
∴△DFC是等腰直角三角形.
(法二)如图(3),过F分别作FN⊥BC的延长线于N,FP⊥CD于P,

则∠FNE=90°=∠B.
由(1)知,∠3=∠2,EF=AE,
在△FNE和△EBA中,
|
∴△FNE≌△EBA(AAS),
∴FN=BE=
| 1 |
| 2 |
| 1 |
| 2 |
易证四边形FNCP为矩形(正方形),
则CP=FN=
| 1 |
| 2 |
∴FP垂直平分CD,
∴FD=FC.
∵∠DCF=
| 1 |
| 2 |
∴∠FDC=∠DCF=45°,
∴△DFC是等腰直角三角形.
点评:此题考查正方形的性质,等腰三角形的判定与性质,三角形全等的判定与性质,相似三角形的判定与性质等知识点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若
是方程组
的解,则a+b的值为( )
|
|
A、
| ||
B、
| ||
| C、1 | ||
D、
|

 若反比例函数y1=
若反比例函数y1=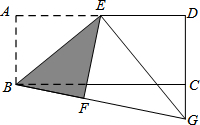 如图,在矩形ABCD中,E是AD的中点,把矩形沿BE折叠,使点A落在矩形外的一点F上,连接BF并延长交DC的延长线于点G.
如图,在矩形ABCD中,E是AD的中点,把矩形沿BE折叠,使点A落在矩形外的一点F上,连接BF并延长交DC的延长线于点G. 如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,联结DC.如果AD=2,BD=6,那么△ADC的周长为
如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,联结DC.如果AD=2,BD=6,那么△ADC的周长为