题目内容
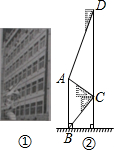 一处中学在教学楼前新建了一座雕塑(如图①).为了测量雕塑的高度,小王在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
一处中学在教学楼前新建了一座雕塑(如图①).为了测量雕塑的高度,小王在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造关系式求解.
解答:解:过点C作CE⊥AB于E.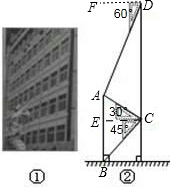
∵∠ADC=90°-60°=30°,∠ACD=90°-30°=60°,
∴∠CAD=90°.
∵CD=10,
∴AC=
CD=5.
在Rt△ACE中,
∵∠AEC=90°,∠ACE=30°,
∴AE=
AC=
,
CE=AC•cos∠ACE=5•cos30°=
.
在Rt△BCE中,
∵∠BCE=45°,
∴BE=CE=
,
∴AB=AE+BE=(
+
)≈6.8(米).
所以,雕塑AB的高度约为6.8米.

∵∠ADC=90°-60°=30°,∠ACD=90°-30°=60°,
∴∠CAD=90°.
∵CD=10,
∴AC=
| 1 |
| 2 |
在Rt△ACE中,
∵∠AEC=90°,∠ACE=30°,
∴AE=
| 1 |
| 2 |
| 5 |
| 2 |
CE=AC•cos∠ACE=5•cos30°=
5
| ||
| 2 |
在Rt△BCE中,
∵∠BCE=45°,
∴BE=CE=
| 5 |
| 2 |
| 3 |
∴AB=AE+BE=(
| 5 |
| 2 |
5
| ||
| 2 |
所以,雕塑AB的高度约为6.8米.
点评:本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
如果xm-1•xm-2•xm-3•x=x7,那么m=( )
| A、4 | B、3 | C、2 | D、1 |
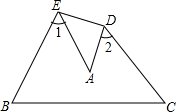 如图,把△ABC纸片沿DE折叠,当A落在四边形BCDE内时,则∠A与∠1+∠2之间有始终不变的关系是( )
如图,把△ABC纸片沿DE折叠,当A落在四边形BCDE内时,则∠A与∠1+∠2之间有始终不变的关系是( )| A、∠A=∠1+∠2 |
| B、2∠A=∠1+∠2 |
| C、3A=∠1+∠2 |
| D、3∠A=2(∠1+∠2) |