题目内容
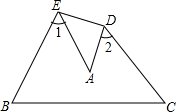 如图,把△ABC纸片沿DE折叠,当A落在四边形BCDE内时,则∠A与∠1+∠2之间有始终不变的关系是( )
如图,把△ABC纸片沿DE折叠,当A落在四边形BCDE内时,则∠A与∠1+∠2之间有始终不变的关系是( )| A、∠A=∠1+∠2 |
| B、2∠A=∠1+∠2 |
| C、3A=∠1+∠2 |
| D、3∠A=2(∠1+∠2) |
考点:三角形内角和定理,翻折变换(折叠问题)
专题:
分析:根据∠1与∠AED的2倍和∠2与∠ADE的2倍都组成平角,结合△AED的内角和为180°可求出答案.
解答:解:∵△ABC纸片沿DE折叠,
∴∠1+2∠AED=180°,∠2+2∠ADE=180°,
∴∠AED=
(180°-∠1),∠ADE=
(180°-∠2),
∴∠AED+∠ADE=
(180°-∠1)+
(180°-∠2)=180°-
(∠1+∠2)
∴△ADE中,∠A=180°-(∠AED+∠ADE)=180°-[180°-
(∠1+∠2)]=
(∠1+∠2),
即2∠A=∠1+∠2.
故选B.
∴∠1+2∠AED=180°,∠2+2∠ADE=180°,
∴∠AED=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AED+∠ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴△ADE中,∠A=180°-(∠AED+∠ADE)=180°-[180°-
| 1 |
| 2 |
| 1 |
| 2 |
即2∠A=∠1+∠2.
故选B.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°及图形翻折变换的性质是解答此题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
甲车行驶40千米与乙车行驶50千米所用时间相同,已知乙车每小时比甲车多行驶15千米.设甲车的速度为x千米/小时,依题意列方程正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,AB∥CD∥EF,∠ABE=38°,∠ECD=110°,则∠BEC的度数为( )
如图,AB∥CD∥EF,∠ABE=38°,∠ECD=110°,则∠BEC的度数为( )| A、42° | B、32° |
| C、62° | D、38° |
已知线段AB=8cm,点C是直线AB上一点,且线段BC=3cm,则线段AC的长是( )
| A、5cm | B、11cm |
| C、5cm或11cm | D、不能确定 |
气温由-5℃上升2℃后是( )
| A、-3℃ | B、3℃ |
| C、7℃ | D、-7℃ |
三条线段满足
=
,若a=2,c=8,则b的长度为( )
| a |
| b |
| b |
| c |
| A、±4 | B、4 | C、2 | D、6 |
 已知:如图1:点A(5,0)B(0,2),AB=AC,∠BAC=90°.
已知:如图1:点A(5,0)B(0,2),AB=AC,∠BAC=90°.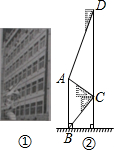 一处中学在教学楼前新建了一座雕塑(如图①).为了测量雕塑的高度,小王在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
一处中学在教学楼前新建了一座雕塑(如图①).为了测量雕塑的高度,小王在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据