题目内容
20.已知a+b=5,a2+b2=19,则ab=3.分析 把a+b=5两边平方,然后把a2+b2=19代入即可求解.
解答 解:∵a+b=5,
∴(a+b)2=25,即a2+b2+2ab=25,
∴19+2ab=25,
解得:ab=3.
故答案是:3.
点评 本题主要考查完全平方公式的变形,熟记公式结构是解题的关键.完全平方公式:(a±b)2=a2±2ab+b2.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
10.对于y=(x-3)2+2的图象下列叙述错误的是( )
| A. | 当x≥2时,y随x增大而增大 | B. | 对称轴为直线x=3 | ||
| C. | 当x=3时,y有最小值2 | D. | 顶点坐标为(3,2) |
11.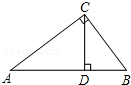 如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,CD⊥AB于点D,sin∠BCD=( )
如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,CD⊥AB于点D,sin∠BCD=( )
 如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,CD⊥AB于点D,sin∠BCD=( )
如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,CD⊥AB于点D,sin∠BCD=( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
9.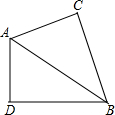 如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
 如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )| A. | SSS | B. | SAS | C. | HL | D. | AAS |
10. 如图,在△ABC中,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线MN,与AB交于点O,以O为圆心,OA为半径作圆,⊙O恰好经过点C.下列结论中,错误的是( )
如图,在△ABC中,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线MN,与AB交于点O,以O为圆心,OA为半径作圆,⊙O恰好经过点C.下列结论中,错误的是( )
 如图,在△ABC中,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线MN,与AB交于点O,以O为圆心,OA为半径作圆,⊙O恰好经过点C.下列结论中,错误的是( )
如图,在△ABC中,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线MN,与AB交于点O,以O为圆心,OA为半径作圆,⊙O恰好经过点C.下列结论中,错误的是( )| A. | AB是⊙O的直径 | B. | ∠ACB=90° | ||
| C. | △ABC是⊙O内接三角形 | D. | O是△ABC的内心 |
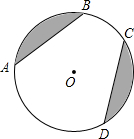 如图,$\widehat{AB}$+$\widehat{CD}$=$\widehat{AD}$+$\widehat{BC}$,弦AB长为8,DC长为4,则S阴影为10π-16.
如图,$\widehat{AB}$+$\widehat{CD}$=$\widehat{AD}$+$\widehat{BC}$,弦AB长为8,DC长为4,则S阴影为10π-16. 平移△ABC,使点A移动到点A′,画出平移后的△A′B′C′.
平移△ABC,使点A移动到点A′,画出平移后的△A′B′C′.