题目内容
10. 如图,在△ABC中,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线MN,与AB交于点O,以O为圆心,OA为半径作圆,⊙O恰好经过点C.下列结论中,错误的是( )
如图,在△ABC中,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线MN,与AB交于点O,以O为圆心,OA为半径作圆,⊙O恰好经过点C.下列结论中,错误的是( )| A. | AB是⊙O的直径 | B. | ∠ACB=90° | ||
| C. | △ABC是⊙O内接三角形 | D. | O是△ABC的内心 |
分析 利用作法可判断点O为AB的中点,则可判断AB为⊙O的直径,根据圆周角定理得到∠ACB=90°,根据三角形内接圆的定义得到△ABC为⊙O的内接三角形,然后对选项进行判断.
解答 解:由作法得MN垂直平分AB,则OA=OB,则AB为⊙O的直径,
∵⊙O恰好经过点C,
∴∠ACB=90°,△ABC为⊙O的内接三角形,点O为△ABC的外心.
故选D.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.解决本题的关键是理解三角形的内心的定义.

练习册系列答案
相关题目
1. 如图,在不添加任何线的情况下,图中一定存在( )
如图,在不添加任何线的情况下,图中一定存在( )
 如图,在不添加任何线的情况下,图中一定存在( )
如图,在不添加任何线的情况下,图中一定存在( )| A. | 同位角 | B. | 内错角 | C. | 同旁内角 | D. | 以上角都不存在 |
18.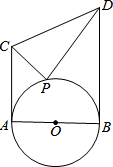 如图,⊙O的半径为1,AC⊥AB于A,BD⊥AB于B,AC=2,BD=3,P为半圆上一点,则△PCD面积的最小值是( )
如图,⊙O的半径为1,AC⊥AB于A,BD⊥AB于B,AC=2,BD=3,P为半圆上一点,则△PCD面积的最小值是( )
 如图,⊙O的半径为1,AC⊥AB于A,BD⊥AB于B,AC=2,BD=3,P为半圆上一点,则△PCD面积的最小值是( )
如图,⊙O的半径为1,AC⊥AB于A,BD⊥AB于B,AC=2,BD=3,P为半圆上一点,则△PCD面积的最小值是( )| A. | $\frac{3}{2}$ | B. | $\frac{9}{5}$ | C. | $\frac{{\sqrt{5}}}{4}$ | D. | $\frac{{5-\sqrt{5}}}{2}$ |
2. 如图所示的几何体是由5个相同的小正方体组成,其主视图为( )
如图所示的几何体是由5个相同的小正方体组成,其主视图为( )
 如图所示的几何体是由5个相同的小正方体组成,其主视图为( )
如图所示的几何体是由5个相同的小正方体组成,其主视图为( )| A. |  | B. |  | C. |  | D. |  |
19. 某商品的外包装盒的三视图如图所示,则这个包装盒的侧面积为( )
某商品的外包装盒的三视图如图所示,则这个包装盒的侧面积为( )
 某商品的外包装盒的三视图如图所示,则这个包装盒的侧面积为( )
某商品的外包装盒的三视图如图所示,则这个包装盒的侧面积为( )| A. | 150πcm2 | B. | 200πcm2 | C. | 300πcm2 | D. | 400πcm2 |
20. 如图所示,有一“工”字形的机器零件,它是轴对称图形,图中所有的角都是直角,图中数据单位:cm,那么A.B两点之间的距离为( )
如图所示,有一“工”字形的机器零件,它是轴对称图形,图中所有的角都是直角,图中数据单位:cm,那么A.B两点之间的距离为( )
 如图所示,有一“工”字形的机器零件,它是轴对称图形,图中所有的角都是直角,图中数据单位:cm,那么A.B两点之间的距离为( )
如图所示,有一“工”字形的机器零件,它是轴对称图形,图中所有的角都是直角,图中数据单位:cm,那么A.B两点之间的距离为( )| A. | 8cm | B. | 8$\sqrt{2}$cm | C. | 16cm | D. | 16$\sqrt{2}$cm |
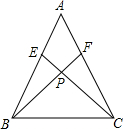 在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:△EBC≌△FCB.
在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:△EBC≌△FCB.