题目内容
11.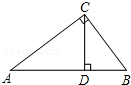 如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,CD⊥AB于点D,sin∠BCD=( )
如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,CD⊥AB于点D,sin∠BCD=( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
分析 首先利用互余两角的关系得出∠A=∠BCD,进而利用锐角三角函数关系求出即可.
解答 解:∵∠ACB=90°,CD⊥AB,
∵∠BCD+∠B=90°,∠A+∠B=90°,
∴∠A=∠BCD,
∴sin∠BCD=sinA=$\frac{BC}{AB}=\frac{3}{5}$,
故选B.
点评 此题主要考查了锐角三角函数关系的定义,得出sin∠BCD=sinA是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列各组数的大小正确的是( )
| A. | -$\frac{2}{3}$<-$\frac{3}{5}$ | B. | -1.5>-1.4 | C. | -(-$\frac{13}{6}$)<-(-$\frac{1}{15}$) | D. | 3<-1 |
1. 如图,在不添加任何线的情况下,图中一定存在( )
如图,在不添加任何线的情况下,图中一定存在( )
 如图,在不添加任何线的情况下,图中一定存在( )
如图,在不添加任何线的情况下,图中一定存在( )| A. | 同位角 | B. | 内错角 | C. | 同旁内角 | D. | 以上角都不存在 |
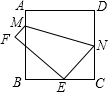 如图所示,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在E处,折痕为MN,则线段CN的长是3cm.
如图所示,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在E处,折痕为MN,则线段CN的长是3cm.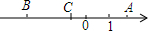 有理数a、b、c在数轴上对应的点分别是A、B、C,其位置如图所示.试化简:
有理数a、b、c在数轴上对应的点分别是A、B、C,其位置如图所示.试化简: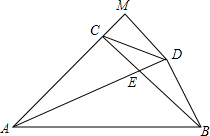 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连CD,下列五个结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连CD,下列五个结论: