题目内容
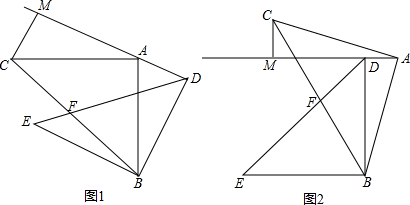
已知如图1,△ABC和△DBE都是等腰直角三角形,线段CB、DE相交于点F,点A在平行于BE的直线AD上,过点C作CM⊥AD于M.
(1)当点A在点D的左侧时,求证:CM=AD;
(2)如图2,当点A在点D的右侧时,点B关于DE的对称点落在直线AD的G点处,当CF=13时,求线段GF的长.
(1)当点A在点D的左侧时,求证:CM=AD;
(2)如图2,当点A在点D的右侧时,点B关于DE的对称点落在直线AD的G点处,当CF=13时,求线段GF的长.

考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)根据全等三角形的判定定理证明一对三角形全等,即可解决问题.
(2)通过证明一对三角形全等得到两个角相等,进而证明四点共圆;借助圆内接四边形的性质及正方形的性质即可解决问题.
(2)通过证明一对三角形全等得到两个角相等,进而证明四点共圆;借助圆内接四边形的性质及正方形的性质即可解决问题.
解答: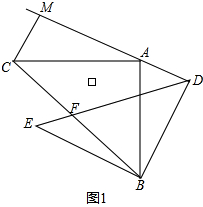 解:(1)如图1,∵△ABC,△BDE均是等腰直角三角形,
解:(1)如图1,∵△ABC,△BDE均是等腰直角三角形,
∴AC=AB,∠BAC=∠DBE=90°;
又∵AD∥BE,CM⊥AD,
∴∠ADB+∠DBE=180°,∠AMC=90°,
∴∠ADB=180°-90°=90°,
故∠ADB=∠AMC=90°;
∵∠CAB=90°,
∴∠MCA+∠CAM=∠DAB+∠CAB=90°,
∴∠MCA=∠DAB;
在△MCA与△DAB中,
,
∴△MCA≌△DAB(AAS),
∴CM=AD.
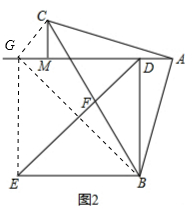 (2)如图2,连接BG、EG、CG;
(2)如图2,连接BG、EG、CG;
∵CM⊥AM,∠CAB=90°,
∴∠MCA+∠MAC=∠MAC+∠DAB=90°,
∴∠MCA=∠DAB;
在△MCA与△DAB中,
,
∴△MCA≌△DAB(AAS),
∴∠CAG=∠ABD;
∵B、G两点关于DE对称,
∴DG=DB,EB=EG;
而EB=DB,
∴DG=DB=EB=EG,
而∠DBE=90°,
∴四边形BDGE为正方形,∠DBG=45°,
而∠ABC=45°,
∴∠CBG=∠ABD,
而∠CAG=∠ABD,
∴∠CBG=∠CAG,
故A、B、G、C四点共圆;
∵∠CAB=90°,
∴∠BGC=180°-90°=90°;
∵B、G两点关于DE对称,
∴FG=FB,
∴∠FGB=∠FBG;
而∠FBG+∠FCG=∠FGB+∠FGC=90°,
∴∠FCG=∠FGC,
故GF=CF,
而CF=13,
∴GF=13.
 解:(1)如图1,∵△ABC,△BDE均是等腰直角三角形,
解:(1)如图1,∵△ABC,△BDE均是等腰直角三角形,∴AC=AB,∠BAC=∠DBE=90°;
又∵AD∥BE,CM⊥AD,
∴∠ADB+∠DBE=180°,∠AMC=90°,
∴∠ADB=180°-90°=90°,
故∠ADB=∠AMC=90°;
∵∠CAB=90°,
∴∠MCA+∠CAM=∠DAB+∠CAB=90°,
∴∠MCA=∠DAB;
在△MCA与△DAB中,
|
∴△MCA≌△DAB(AAS),
∴CM=AD.
 (2)如图2,连接BG、EG、CG;
(2)如图2,连接BG、EG、CG;∵CM⊥AM,∠CAB=90°,
∴∠MCA+∠MAC=∠MAC+∠DAB=90°,
∴∠MCA=∠DAB;
在△MCA与△DAB中,
|
∴△MCA≌△DAB(AAS),
∴∠CAG=∠ABD;
∵B、G两点关于DE对称,
∴DG=DB,EB=EG;
而EB=DB,
∴DG=DB=EB=EG,
而∠DBE=90°,
∴四边形BDGE为正方形,∠DBG=45°,
而∠ABC=45°,
∴∠CBG=∠ABD,
而∠CAG=∠ABD,
∴∠CBG=∠CAG,
故A、B、G、C四点共圆;
∵∠CAB=90°,
∴∠BGC=180°-90°=90°;
∵B、G两点关于DE对称,
∴FG=FB,
∴∠FGB=∠FBG;
而∠FBG+∠FCG=∠FGB+∠FGC=90°,
∴∠FCG=∠FGC,
故GF=CF,
而CF=13,
∴GF=13.
点评:该题考查了全等三角形的判定及其性质、等腰直角三角形的性质及其应用问题;同时,还渗透了对四点共圆的判定、正方形的性质等几何知识的考查;对分析问题解决问题的能力提出了更高的要求.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
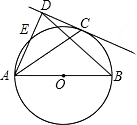 如图,已知AB为⊙O直径,DC与⊙O相切于点C,AD⊥DC于D,AD交⊙O于E.
如图,已知AB为⊙O直径,DC与⊙O相切于点C,AD⊥DC于D,AD交⊙O于E.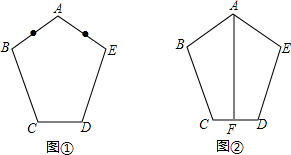 如图①,已知五边形ABCDE,AB=AE,BC=ED,∠ABC=∠AED.
如图①,已知五边形ABCDE,AB=AE,BC=ED,∠ABC=∠AED. 如图,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,试探究线段BE和CD的数量关系,并证明你的结论.
如图,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,试探究线段BE和CD的数量关系,并证明你的结论. 如图,AB∥CD,DF交AC于点F,DE=EF,求证:AE=EC.
如图,AB∥CD,DF交AC于点F,DE=EF,求证:AE=EC.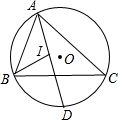 如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于D,∠ABC的平分线交直线AD于I.
如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于D,∠ABC的平分线交直线AD于I.