题目内容
 如图,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,试探究线段BE和CD的数量关系,并证明你的结论.
如图,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,试探究线段BE和CD的数量关系,并证明你的结论.考点:全等三角形的判定与性质,等腰直角三角形
专题:计算题
分析:CD=2BE,理由为:延长BE交CA延长线于F,由CD为角平分线得到一对角相等,再由一对直角相等,CE为公共边,利用ASA得到三角形CEF与三角形CEB全等,利用全等三角形对应边相等得到FE=BE,利用等角的余角相等得到一对角相等,再由一对直角相等,利用ASA得到三角形ABF与三角形ACD全等,利用全等三角形的性质得到CD=BF,等量代换即可得证.
解答: 解:CD=2BE,理由为:
解:CD=2BE,理由为:
延长BE交CA延长线于F,
∵CD平分∠ACB,
∴∠FCE=∠BCE,
在△CEF和△CEB中,
,
∴△CEF≌△CEB(ASA),
∴FE=BE,
∵∠DAC=∠CEF=90°,
∴∠ACD+∠F=∠ABF+∠F=90°,
∴∠ACD=∠ABF,
在△ACD和△ABF中,
,
∴△ACD≌△ABF(ASA),
∴CD=BF,
∴CD=2BE.
 解:CD=2BE,理由为:
解:CD=2BE,理由为:延长BE交CA延长线于F,
∵CD平分∠ACB,
∴∠FCE=∠BCE,
在△CEF和△CEB中,
|
∴△CEF≌△CEB(ASA),
∴FE=BE,
∵∠DAC=∠CEF=90°,
∴∠ACD+∠F=∠ABF+∠F=90°,
∴∠ACD=∠ABF,
在△ACD和△ABF中,
|
∴△ACD≌△ABF(ASA),
∴CD=BF,
∴CD=2BE.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 一个几何体是由一些大小相同的小正方体摆成的,其主视图与俯视图如图,则组成这个几何体的小正方体的块数n的最大值为
一个几何体是由一些大小相同的小正方体摆成的,其主视图与俯视图如图,则组成这个几何体的小正方体的块数n的最大值为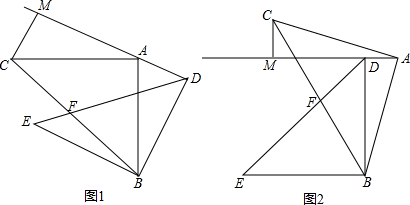
 如图,已知AB=AC,BD=CD,试说明∠B=∠C的理由.
如图,已知AB=AC,BD=CD,试说明∠B=∠C的理由. 如图所示,将△ABC沿直线BC方向平移△DEF的位置,G是DE上一点,连接AG,过点A、D作直线MN.
如图所示,将△ABC沿直线BC方向平移△DEF的位置,G是DE上一点,连接AG,过点A、D作直线MN.