题目内容
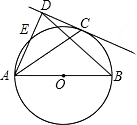 如图,已知AB为⊙O直径,DC与⊙O相切于点C,AD⊥DC于D,AD交⊙O于E.
如图,已知AB为⊙O直径,DC与⊙O相切于点C,AD⊥DC于D,AD交⊙O于E.(1)求证:AC平分∠DAB;
(2)若CD=12,AD=16,求BD的长.
考点:切线的性质
专题:
分析:(1)连接OC,由直线CD与⊙O相切于点C,AD⊥CD,易证得OC∥AD,继而可得AC平分∠DAB;
(2)连接BC,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例以及余弦定理,即可求得答案.
(2)连接BC,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例以及余弦定理,即可求得答案.
解答: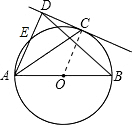 (1)证明:连接OC.
(1)证明:连接OC.
∵直线DC与⊙O相切于点C,
∴OC⊥CD,
∵AD⊥DC,
∴OC∥AD,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠OAC=∠DAC,
即AC平分∠DAB;
(2)解:连接BC.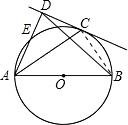
在△ACD中,∵∠ADC=90°,CD=12,AD=16,
∴AC=
=20.
∵AB是⊙O的直径,
∴∠ACB=90°.
在△ADC与△ACB中,
,
∴△ADC∽△ACB,
∴
=
,
即
=
,
解得:BC=15.
在△BCD中,∵BC=15,CD=12,∠BCD=∠ACB+∠ACD=90°+∠ACD,
∴BD2=BC2+CD2-2BC•CD•cos∠BCD
=152+122-2×15×12•cos(90°+∠ACD)
=225+144-360•[-sin∠ACD]
=225+144+360×
=225+144+288
=657,
∴BD=
=3
.
 (1)证明:连接OC.
(1)证明:连接OC.∵直线DC与⊙O相切于点C,
∴OC⊥CD,
∵AD⊥DC,
∴OC∥AD,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠OAC=∠DAC,
即AC平分∠DAB;
(2)解:连接BC.

在△ACD中,∵∠ADC=90°,CD=12,AD=16,
∴AC=
| AD2+CD2 |
∵AB是⊙O的直径,
∴∠ACB=90°.
在△ADC与△ACB中,
|
∴△ADC∽△ACB,
∴
| CD |
| BC |
| AD |
| AC |
即
| 12 |
| BC |
| 16 |
| 20 |
解得:BC=15.
在△BCD中,∵BC=15,CD=12,∠BCD=∠ACB+∠ACD=90°+∠ACD,
∴BD2=BC2+CD2-2BC•CD•cos∠BCD
=152+122-2×15×12•cos(90°+∠ACD)
=225+144-360•[-sin∠ACD]
=225+144+360×
| 16 |
| 20 |
=225+144+288
=657,
∴BD=
| 657 |
| 73 |
点评:此题考查了切线的性质、相似三角形的判定与性质、勾股定理以及余弦定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 一个几何体是由一些大小相同的小正方体摆成的,其主视图与俯视图如图,则组成这个几何体的小正方体的块数n的最大值为
一个几何体是由一些大小相同的小正方体摆成的,其主视图与俯视图如图,则组成这个几何体的小正方体的块数n的最大值为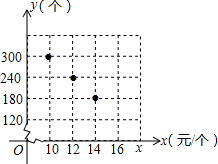 某商店准备购进一批茶杯进行销售,根据市场调查,这种茶杯一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:
某商店准备购进一批茶杯进行销售,根据市场调查,这种茶杯一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示: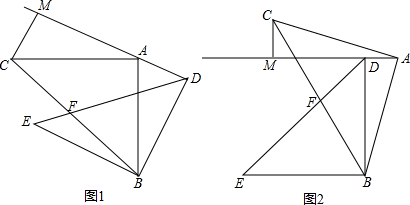
 如图,把一个长方形的纸片沿EF折叠后,点D、C分别落在点M、N的位置,如果∠EFB=65°,那么∠AEM等于
如图,把一个长方形的纸片沿EF折叠后,点D、C分别落在点M、N的位置,如果∠EFB=65°,那么∠AEM等于