题目内容
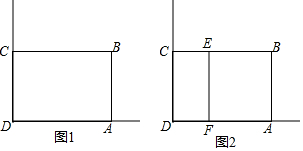
18.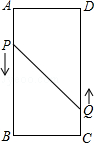 如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(2)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
分析 (1)如图,过点P作PE⊥CD于E,设x秒后PQ=10cm,利用勾股定理得出即可.
(2)分类讨论:①当点P在AB上时;②当点P在BC边上;③当点P在CD边上时.
解答 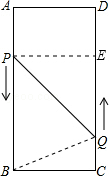 解:(1)过点P作PE⊥CD于E.则根据题意,得
解:(1)过点P作PE⊥CD于E.则根据题意,得
设x秒后,点P和点Q的距离是10cm.
(16-2x-3x)2+62=102,即(16-5x)2=64,
∴16-5x=±8,
∴x1=$\frac{8}{5}$,x2=$\frac{24}{5}$;
∴经过$\frac{8}{5}$s或$\frac{24}{5}$sP、Q两点之间的距离是10cm;
(2)连接BQ.设经过ys后△PBQ的面积为12cm2.
①当0≤y≤$\frac{16}{3}$时,则PB=16-3y,
∴$\frac{1}{2}$PB•BC=12,即$\frac{1}{2}$×(16-3y)×6=12,
解得y=4;
②当$\frac{16}{3}$<x≤$\frac{22}{3}$时,
BP=3y-AB=3y-16,QC=2y,则
$\frac{1}{2}$BP•CQ=$\frac{1}{2}$(3y-16)×2y=12,
解得y1=6,y2=-$\frac{2}{3}$(舍去);
③$\frac{22}{3}$<x≤8时,
QP=CQ-PQ=22-y,则
$\frac{1}{2}$QP•CB=$\frac{1}{2}$(22-y)×6=12,
解得y=18(舍去).
综上所述,经过4秒或6秒△PBQ的面积为 12cm2.
点评 此题主要考查了矩形的性质以及勾股定理和一元二次方程的应用等知识,熟练应用矩形的性质是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.一元二次方程(x-2)2=1可转化为两个一元一次方程,其中一个一元一次方程是x-2=-1,则另一个一元一次方程是( )
| A. | x-2=1 | B. | x+2=1 | C. | x+2=-1 | D. | x-2=-1 |
3.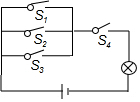 如图,随机闭合开关S1、S2、S3、S4中的两个,则灯泡发光的概率是( )
如图,随机闭合开关S1、S2、S3、S4中的两个,则灯泡发光的概率是( )
 如图,随机闭合开关S1、S2、S3、S4中的两个,则灯泡发光的概率是( )
如图,随机闭合开关S1、S2、S3、S4中的两个,则灯泡发光的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
10.若实数x,y满足(x+2y)2-2x-4(y+1)=-5,则下列式子一定成立的是( )
| A. | x+2y=-1 | B. | x-2y=-1 | C. | x+2y=1 | D. | x-2y=1 |
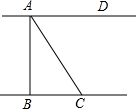 如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=70°,测得BC=7m,则桥长AB=19m(结果精确到1m).
如图,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=70°,测得BC=7m,则桥长AB=19m(结果精确到1m).
 如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为3cm2,则△BEF的面积=$\frac{3}{4}$cm2.
如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为3cm2,则△BEF的面积=$\frac{3}{4}$cm2.