题目内容
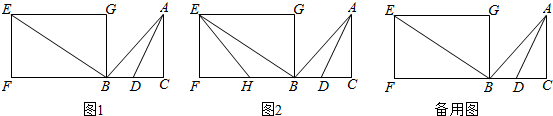
13. 在△ABC中,∠ACB=90°,∠B=60°,AC=6,点D、E在AB边上,AD=CD,点E关于AC、CD的对称点分别为F、G,则线段FG的最小值等于( )
在△ABC中,∠ACB=90°,∠B=60°,AC=6,点D、E在AB边上,AD=CD,点E关于AC、CD的对称点分别为F、G,则线段FG的最小值等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据轴对称的性质得出CE=CF,∠CEF=∠CFE,CE=CG,EH=GH,∠CEF=∠CGH,进而得出CE=CG=CF,∠CGH=∠CFE,然后证得△BCD是等边三角形,从而证得∠FHG=60°,进一步证得∠FCG=∠FHG=60°,证得△CFG是等边三角形,得出FG=CF=CE,因为CE的最小值为3,所以FG的最小值为3.
解答  解:∵点E和F关于AC对称,
解:∵点E和F关于AC对称,
∴AC垂直平分EF,
∴CE=CF,∠CEF=∠CFE,
∵点E和G关于CD对称,设CD交EF于H,AC交EG于S,交EF于K.
∴CD垂直平分EG,
∴CE=CG,EH=GH,∠CEH=∠CGH,
∴CE=CG=CF,
∵∠ACB=90°,∠B=60°,
∴∠A=30°,
∵AD=CD,
∴∠ACD=∠A=30°,
∴∠BCD=60°,
∴△BCD是等边三角形,
∵EF∥BC,
∴∠DEK=∠B=60°,∠EHD=∠BCD=60°,
∴∠DHG=∠EHD=60°,
∴∠FHG=60°
∵∠CGH=∠CFE,∠CKF=∠HKG,
∴∠FCG=∠FHG=60°,
∵CF=CG,
∴△CFG是等边三角形,
∴FG=CF=CE,
∵当CE⊥AB时,CE最短,此时CE=$\frac{1}{2}$AC=3,
∴FG的最小值为3,
故选B.
点评 本题考查了轴对称的性质和等边三角形的判定和性质,证得△CFG是等边三角形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.a和b都是个位数字和十位数字相同的两位数,c是各位数字都相同的四位数,且a2+b=c,则a+b-c的最大值和最小值的差是( )
| A. | 6600 | B. | 3179 | C. | 6723 | D. | 3187 |
4.从图1到图2的拼图过程中,所反映的关系式是( )


| A. | x2+5x+6=(x+2)(x+3) | B. | x2+5x-6=(x+6)(x-1) | C. | x2-5x+6=(x-2)(x-3) | D. | (x+2)(x+3)=x2+5x+6 |
5.用符号f(x)表示关于自然数x的代数式.我们规定:当x为偶数时,f(x)=$\frac{x}{2}$;当x为奇数时,f(x)=3x+1.例如:f(1)=3×1+1=4,f(8)=$\frac{8}{2}$=4.设x1=8,x2=f(x1),x3=f(x2),…,xn=f(xn-1).以此规律,得到一列数x1,x2,x3,…,x2017,则这2017个数之和x1+x2+x3+…+x2016+x2017等于( )
| A. | 4714 | B. | 4712 | C. | 3612 | D. | 3624 |
2.如果(a-b-3)(a-b+3)=40,那么a-b的值为( )
| A. | 49 | B. | 7 | C. | -7 | D. | 7或-7 |
 如果将一副三角板按如图方式叠放,那么∠1=105°.
如果将一副三角板按如图方式叠放,那么∠1=105°.