Question

6．在△ABC中，AD是BC边上的高，⊙P是△ABC的外接圆．
（1）如图1，若AD=5，BD=1，BC=6，求⊙P的半径；
（2）如图2，若∠ABC=75°，∠ACB=45°，I是△ABC的内心，求$\frac{AI}{AP}$的值；
（3）如图3，若∠ABC-∠ACB=30°，当B，C运动时，$\frac{DC-BD}{AP}$的值是否变化？若不变，求出其值；若变化，求出其变化的范围．

Answer 1

分析 （1）过点P作PH⊥BC于点H，连接PA、PC、PD，在直角△PHC中即可解出半径长度；
（2）延长AI交⊙P于点E，连接PE交BC于点F，连接CE、PB、PC、IC，过点B作BH⊥AC于点H，利用边角关系，用AP表示出来AI，即可解决；
（3）过点A作AE∥BC，交⊙P于点E，连接PE、CE，过点E作EF⊥BC于点F，借助△ABD≌△ECF找出边角关系，用AP表示出DC和BD即可得出结论．

解答 解：（1）过点P作PH⊥BC于点H，连接PA、PC、PD，如图1，

∵∠ACB=45°，
∴CD=AD=5，
在△PAD和△PCD中，$\left\{\begin{array}{l}{PA=PC（半径）}\\{CD=AD}\\{PD=PD}\end{array}\right.$，
∴△PAD≌△PCD（SSS），
∴∠PDC=∠PDA=45°，
∴PH=DH=BH-BD=2，
又∵CH=3，
∴由勾股定理知：PC=$\sqrt{P{H}^{2}+C{H}^{2}}$=$\sqrt{13}$．
（2）延长AI交⊙P于点E，连接PE交BC于点F，连接CE、PB、PC、IC，过点B作BH⊥AC于点H，如图2，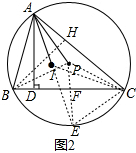

∠EIC=∠IAC+∠ICA=52.5°，∠ECI=∠BCE+∠ICB=52.5°，
∴∠EIC=∠ECI，
∴EI=EC，
∵∠EPC=2∠CAE=60°（圆心角等于圆周角的2倍），
∴△PCE是等边三角形，
∴CE=PC=AP，
∴IE=AP，
∵∠CAE=30°，∠ACE=75°，
∴∠AEC=75°=∠ACE，
∴AC=AE=AI+IE=AI+AP，
∵∠BAE=∠CAE，
∴$\widehat{BE}$=$\widehat{CE}$，
∴PE⊥BC，
∴BC=2BF=2×$\frac{\sqrt{3}}{2}$PB=$\sqrt{3}$AP，
∴CH=$\frac{\sqrt{2}}{2}$BC=$\frac{\sqrt{6}}{2}$AP，
又∵AH=$\frac{\sqrt{3}}{3}$BH=$\frac{\sqrt{3}}{3}$CH=$\frac{\sqrt{2}}{2}$AP，
∴AI+AP=AC=$\frac{\sqrt{2}}{2}$AP+$\frac{\sqrt{6}}{2}$AP，
∴$\frac{AI}{AP}$=$\frac{\sqrt{2}+\sqrt{6}-2}{2}$．
（3）过点A作AE∥BC，交⊙P于点E，连接PE、CE，过点E作EF⊥BC于点F，如图3，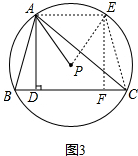

∵AE∥BC，
∴$\widehat{AB}$=$\widehat{CE}$，
∴AB=CE，
∵四边形ADFE是矩形，
∴AE=DF，AD=EF，
∴△ABD≌△ECF，
∴BD=CF，∠ABD=∠ECF，
∴∠ACE=∠ECB-∠ACB=∠ABC-∠ACB=30°，
∴∠APE=2∠ACE=60°，
∴AP=AE=DF，
∴$\frac{DC-BD}{AP}$=$\frac{DC-CF}{AP}$=$\frac{DF}{AP}$=1．
故当B，C运动时，$\frac{DC-BD}{AP}$的值是不变，$\frac{DC-BD}{AP}$=1．

点评 本题考查了圆心角与圆周角的关系、勾股定义以及三角形全等的判定与性质定理等，解题的关键是画出图形，借助于数形结合解决问题．