题目内容
18.计算(1)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$
(2)(-3)0-$\sqrt{27}$+|1-$\sqrt{2}$|+$\frac{1}{\sqrt{3}+\sqrt{2}}$
(3)(3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$)÷2$\sqrt{3}$
(4)($\sqrt{32}$-3$\sqrt{3}$)(4$\sqrt{2}$+$\sqrt{27}$)
分析 (1)根据二次根式混合运算法则化简即可.
(2)根据零次幂的意义、绝对值的定义、分母有理化的法则,化简然后合并同类二次根式即可.
(3)先计算括号后计算除法.
(4)利用平方差公式计算.
解答 解:(1)原式=4-$\sqrt{6}$+2$\sqrt{6}$=4+$\sqrt{6}$.
(2)原式=1-3$\sqrt{3}$+$\sqrt{2}$-1+$\sqrt{3}-\sqrt{2}$=-2$\sqrt{3}$.
(3)原式=(6$\sqrt{3}$-$\frac{2}{3}$$\sqrt{3}$+4$\sqrt{3}$)÷2$\sqrt{3}$=$\frac{28}{3}\sqrt{3}$$÷2\sqrt{3}$=$\frac{14}{3}$.
(4)原式=(4$\sqrt{2}$-3$\sqrt{3}$)(4$\sqrt{2}$+3$\sqrt{3}$)=(4$\sqrt{2}$)2-(3$\sqrt{3}$)2=32-27=5.
点评 本题考查二次根式的混合运算法则、零指数的性质、绝对值的定义,灵活应用法则或公式是解决问题的关键,计算时注意符号问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.一次函数y=-x+1的图象不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.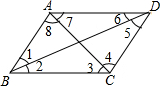 如图,由已知条件推出的结论,正确的是( )
如图,由已知条件推出的结论,正确的是( )
 如图,由已知条件推出的结论,正确的是( )
如图,由已知条件推出的结论,正确的是( )| A. | 由∠1=∠5,可以推出AD∥CB | B. | 由∠4=∠8,可以推出AD∥BC | ||
| C. | 由∠2=∠6,可以推出AD∥BC | D. | 由∠3=∠7,可以推出AB∥DC |
10.在|-2|,0,1,-1这四个数中,最大的数是( )
| A. | |-2| | B. | 0 | C. | 1 | D. | -1 |
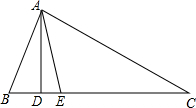 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求: