题目内容
 如图,在正△ABC中,D、E分别是BC、AC上一点,AE=CD,AD与BE交于点F,AF=
如图,在正△ABC中,D、E分别是BC、AC上一点,AE=CD,AD与BE交于点F,AF=| 1 |
| 2 |
考点:全等三角形的判定与性质,三角形的外角性质,等腰三角形的性质
专题:证明题
分析:首先易得△ABE≌△CAD(SAS),得出∠1=∠6,BE=AD,∠AEB=∠ADC,然后取BF中点M,得到AF=BM,从而得出△AME≌△CFD(SAS),利用外角的性质,等腰三角形的性质,得到∠8与∠1+∠2的关系以及∠BAE与∠1+∠2的关系,利用∠BAE=60°,可得∠8的度数以及∠3的读数,从而得到∠BFC的读数,最后可得CF⊥BE.
解答: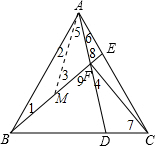 证明:取BF中点M,连接AM.
证明:取BF中点M,连接AM.
在△ABE和△CAD中,∠EAB=∠DCA=60°,AB=CA,
,
∴△ABE≌△CAD(SAS)
∴∠1=∠6,BE=AD,∠AEB=∠ADC,
∵AF=
BF,BM=
BF,
∴AF=BM.
∵FD=AD-AF,ME=BE-BM,
∴FD=ME.
在△AME与△CFD中,
,
∴△AME≌△CFD(SAS),
∴∠7=∠MAE=∠5+∠6,∠3=∠4,
∵AF=MF,
∴∠8=∠3+∠5=2(∠1+∠2),
而∠BAE=∠2+∠5+∠6=∠2+∠3+∠6=∠2+(∠1+∠2)+∠1=2(∠1+∠2),
∴∠8=∠9=60°,∠3=∠1+∠2=
∠BAE=30°,
又∵∠9=∠8=60°,∠4=∠3=30°,
∴∠BFC=∠9+∠4=90°,
∴CF⊥BE.
 证明:取BF中点M,连接AM.
证明:取BF中点M,连接AM.在△ABE和△CAD中,∠EAB=∠DCA=60°,AB=CA,
|
∴△ABE≌△CAD(SAS)
∴∠1=∠6,BE=AD,∠AEB=∠ADC,
∵AF=
| 1 |
| 2 |
| 1 |
| 2 |
∴AF=BM.
∵FD=AD-AF,ME=BE-BM,
∴FD=ME.
在△AME与△CFD中,
|
∴△AME≌△CFD(SAS),
∴∠7=∠MAE=∠5+∠6,∠3=∠4,
∵AF=MF,
∴∠8=∠3+∠5=2(∠1+∠2),
而∠BAE=∠2+∠5+∠6=∠2+∠3+∠6=∠2+(∠1+∠2)+∠1=2(∠1+∠2),
∴∠8=∠9=60°,∠3=∠1+∠2=
| 1 |
| 2 |
又∵∠9=∠8=60°,∠4=∠3=30°,
∴∠BFC=∠9+∠4=90°,
∴CF⊥BE.
点评:本题考查了全等三角形的判定与性质、三角形的外角性质、等腰三角形的性质的应用,解题的关键在于作出相关辅助线,利用角的关系进行解答.

练习册系列答案
相关题目
 如图,已知⊙O是△ABC的外接圆,点I是△ABC的内心,延长AI交BC于点E,交⊙O于点D,连接BD、DC、BI.求证:DB=DC=DI.
如图,已知⊙O是△ABC的外接圆,点I是△ABC的内心,延长AI交BC于点E,交⊙O于点D,连接BD、DC、BI.求证:DB=DC=DI.
 如图为6个边长相等的正方形的组合图形,则∠1+∠3=
如图为6个边长相等的正方形的组合图形,则∠1+∠3=