题目内容
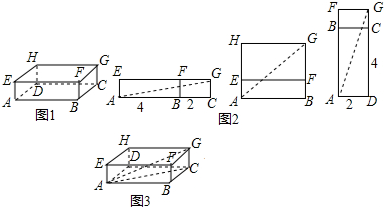
如图1,是一个长方体盒子,长AB=4,宽BC=2,高CG=1.
(1)一只蚂蚁从盒子下底面的点A沿盒子表面爬到点G,求它所行走的最短路线的长.
(2)这个长方体盒子内能容下的最长木棒长度的为多少?
解:(1)蚂蚁从点A爬到点G有三种可能,展开成平面图形如图2所示,由勾股定理计算出AG2的值分别为 、 、 ,比较后得AG2最小为 .即最短路线的长是 .
(2)如图3,AG2=AC2+CG2=AB2+BC2+CG2=42+22+12=21.
(1)一只蚂蚁从盒子下底面的点A沿盒子表面爬到点G,求它所行走的最短路线的长.
(2)这个长方体盒子内能容下的最长木棒长度的为多少?
解:(1)蚂蚁从点A爬到点G有三种可能,展开成平面图形如图2所示,由勾股定理计算出AG2的值分别为
(2)如图3,AG2=AC2+CG2=AB2+BC2+CG2=42+22+12=21.

考点:平面展开-最短路径问题
专题:
分析:(1)蚂蚁有三种爬法,就是把正视和俯视(或正视和侧视,或俯视和侧视)二个面展平成一个长方形,然后利用勾股定理求其对角线,比较大小即可求得最短的途径;
(2)根据勾股定理,知长方体盒子内能容下的最长木棒的平方等于长方体的长、宽、高的平方和.
(2)根据勾股定理,知长方体盒子内能容下的最长木棒的平方等于长方体的长、宽、高的平方和.
解答: 解:(1)蚂蚁从点A爬到点G有三种可能,展开成平面图形如图2所示,由勾股定理计算出AG2的值分别为(4+2)2+12=37、42+(1+2)2=25、22+(4+1)2=29,比较后得AG2最小为25.即最短路线的长是5.
解:(1)蚂蚁从点A爬到点G有三种可能,展开成平面图形如图2所示,由勾股定理计算出AG2的值分别为(4+2)2+12=37、42+(1+2)2=25、22+(4+1)2=29,比较后得AG2最小为25.即最短路线的长是5.
(2)如图3,AG2=AC2+CG2=AB2+BC2+CG2=42+22+12=21.
故答案为37,25,29,5.
 解:(1)蚂蚁从点A爬到点G有三种可能,展开成平面图形如图2所示,由勾股定理计算出AG2的值分别为(4+2)2+12=37、42+(1+2)2=25、22+(4+1)2=29,比较后得AG2最小为25.即最短路线的长是5.
解:(1)蚂蚁从点A爬到点G有三种可能,展开成平面图形如图2所示,由勾股定理计算出AG2的值分别为(4+2)2+12=37、42+(1+2)2=25、22+(4+1)2=29,比较后得AG2最小为25.即最短路线的长是5.(2)如图3,AG2=AC2+CG2=AB2+BC2+CG2=42+22+12=21.
故答案为37,25,29,5.
点评:本题考查了平面展开-最短路径问题及勾股定理的应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.注意:长方体中最长的对角线的平方等于长方体的长、宽、高的平方和.

练习册系列答案
相关题目
 如图,在△ABC中,AB⊥AC,垂足为A.
如图,在△ABC中,AB⊥AC,垂足为A.
 如图,Rt△ABC中,以AB为边向外作正方形,以BC为直径向外作半圆,且正方形面积与半圆面积之比为9:2π,现已AC为直角边向外作Rt△ACD,若AD=8,CD=17,则正方形的面积为
如图,Rt△ABC中,以AB为边向外作正方形,以BC为直径向外作半圆,且正方形面积与半圆面积之比为9:2π,现已AC为直角边向外作Rt△ACD,若AD=8,CD=17,则正方形的面积为 如图,在正△ABC中,D、E分别是BC、AC上一点,AE=CD,AD与BE交于点F,AF=
如图,在正△ABC中,D、E分别是BC、AC上一点,AE=CD,AD与BE交于点F,AF= 如图,AB是⊙O的直径,D是⊙O上的任意一点(不与点A、B重合),延长BD到点C,使DC=BD,判断△ABC的形状:
如图,AB是⊙O的直径,D是⊙O上的任意一点(不与点A、B重合),延长BD到点C,使DC=BD,判断△ABC的形状: 如图所示,已知AD:DB=7:2,AC:CE=4:3,则BF:FC=
如图所示,已知AD:DB=7:2,AC:CE=4:3,则BF:FC=