题目内容
8.已知a+b=14,当a,b分别为正整数时,$\frac{a}{b}$能否等于$\frac{1}{2}$?为什么?分析 根据代入消元法,可得方程的解.
解答 解:$\frac{a}{b}$不能等于$\frac{1}{2}$,理由如下:
假设$\frac{a}{b}$=$\frac{1}{2}$,
联立,得
$\left\{\begin{array}{l}{a+b=14①}\\{\frac{a}{b}=\frac{1}{2}②}\end{array}\right.$,
由②,得b=2a ③,
把③代入①,得
3a=14,
a=$\frac{14}{3}$不是正整数,
∴$\frac{a}{b}$≠$\frac{1}{2}$.
点评 本题考查了解二元一次方程组,有加减法和代入法两种,系数相等或互为相反数时一般选用加减法解二元一次方程组较简单.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.下列长度的三条线段,能组成三角形的是( )
| A. | 1,2,3 | B. | 4,5,6 | C. | 7,8,16 | D. | 9,10,20 |
13.下列各组单项式中,不是同类项的是( )
| A. | 3与-2 | B. | -xy与yx | C. | $\frac{1}{3}$a与$\frac{1}{2}$b | D. | $\frac{1}{3}$x2y与$\frac{2}{3}$yx2 |

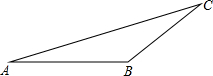 如图,在△ABC中,AB=BC,∠A=15°,求tanA的值.
如图,在△ABC中,AB=BC,∠A=15°,求tanA的值. 如图,∠BAC=90°,AD是BC边的中线,若AB=6,AC=8,则AD=5.
如图,∠BAC=90°,AD是BC边的中线,若AB=6,AC=8,则AD=5.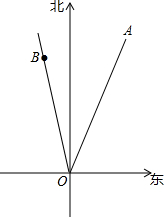 2014年第10号台风“麦德姆”,是2014年度对我国破坏性最大的一次台风,“麦德姆”台风从福建登陆后一路北上,在青岛荣成再次登陆.如图所示,某时,台风“麦德姆”的中心在点O沿北偏东20°的方向以30km/h的速度移动,在点O北偏西10°的方向距离O点360km处有一个小岛B.如果台风中心的最大风力为14级,每远离台风中心20千米风力减弱一级,小岛A的风力达到四级或四级以上,则称其受台风影响.
2014年第10号台风“麦德姆”,是2014年度对我国破坏性最大的一次台风,“麦德姆”台风从福建登陆后一路北上,在青岛荣成再次登陆.如图所示,某时,台风“麦德姆”的中心在点O沿北偏东20°的方向以30km/h的速度移动,在点O北偏西10°的方向距离O点360km处有一个小岛B.如果台风中心的最大风力为14级,每远离台风中心20千米风力减弱一级,小岛A的风力达到四级或四级以上,则称其受台风影响.