题目内容
12.定义一种对正整数n的“F”运算:(1)当n为奇数时,结果是3n+5;(2)n为偶数时,结果是$\frac{n}{{2}^{k}}$(其中k是使$\frac{n}{{2}^{k}}$为奇数的正整数),并且运算重复进行.例如取n=26,则有如图的结果,那么当n=2015,那么第2015次“F”运算的结果是( )
| A. | 5 | B. | 20 | C. | 25 | D. | 18 |
分析 根据运算规则进行重复计算,从中发现循环的规律,得到答案.
解答 解:根据题意,得
当n=2015时,第1次的计算结果是3n+5=6050;
第2次的计算结果是$\frac{6050}{2}$=3025;
第3次的计算结果是3025×3+5=9080;
第4次是计算结果是$\frac{9080}{{2}^{3}}$=1135;
第5次的计算结果是1135×3+5=3410;
第6次的计算结果是$\frac{3410}{2}$=1705,
第7次的计算结果是1705×3+5=5120,
第8次的计算结果是$\frac{5120}{{2}^{10}}$=5,
第9次的计算结果是5×3+5=20,
第10次的计算结果是$\frac{20}{{2}^{2}}$=5,开始循环.
故第2015次的计算结果是20
故选:B.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律即可求出结果.

练习册系列答案
相关题目
18.下列方程是一元一次方程的是( )
| A. | 2x+3y=1 | B. | -2y-1=0 | C. | -x2=2 | D. | 2-3=-1 |
1. 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠AOF的度数是( )
如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠AOF的度数是( )
 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠AOF的度数是( )
如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠AOF的度数是( )| A. | 130° | B. | 120° | C. | 125° | D. | 100° |
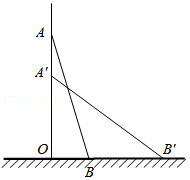 一架方梯AB长2.5米,如图,斜靠在一面墙上,梯子底端离墙OB为0.7米,
一架方梯AB长2.5米,如图,斜靠在一面墙上,梯子底端离墙OB为0.7米, 如图,在矩形ABCD中,对角线AC、BD相交于O,AE⊥BD于点E,已知AB=3,AD=3$\sqrt{3}$,求△AEO的面积.
如图,在矩形ABCD中,对角线AC、BD相交于O,AE⊥BD于点E,已知AB=3,AD=3$\sqrt{3}$,求△AEO的面积.
 如图,已知圆内接四边形ABCD,AD是⊙O的直径,OC⊥BD于E.
如图,已知圆内接四边形ABCD,AD是⊙O的直径,OC⊥BD于E.