题目内容
4.若一元二次方程x2+2x+a=0的有实数解,则a的取值范围是( )| A. | a<1 | B. | a≤4 | C. | a≤1 | D. | a≥1 |
分析 若一元二次方程x2+2x+a=0的有实数解,则根的判别式△≥0,据此可以列出关于a的不等式,通过解不等式即可求得a的值.
解答 解:因为关于x的一元二次方程有实根,
所以△=b2-4ac=4-4a≥0,
解之得a≤1.
故选C.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
15.下列计算正确的是( )
| A. | a2•a3=a6 | B. | $\sqrt{6}$÷$\sqrt{2}$=$\sqrt{3}$ | C. | ($\frac{1}{2}$)-2=-2 | D. | (-a3)2=-a6 |
 如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )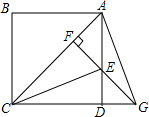 如图,P为正方形ABCD对角线AC上一动点,EF⊥AC且交AD于E,交CD的延长线于点G,连接CE和AG.
如图,P为正方形ABCD对角线AC上一动点,EF⊥AC且交AD于E,交CD的延长线于点G,连接CE和AG.