题目内容
10.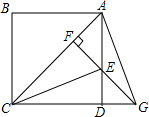 如图,P为正方形ABCD对角线AC上一动点,EF⊥AC且交AD于E,交CD的延长线于点G,连接CE和AG.
如图,P为正方形ABCD对角线AC上一动点,EF⊥AC且交AD于E,交CD的延长线于点G,连接CE和AG.(1)求证:△ADG≌△CDE;
(2)当CE平分∠ACD时,求tan∠AGD.
分析 (1)根据正方形的性质和全等三角形证明△ADG与△CDE全等即可;
(2)设DG为k,利用三角函数的正切值解答即可.
解答 (1)证明:在正方形ABCD中,AD=CD,∠BAD=∠ADC=90°,
∴∠ADG=180°-∠ADC=90°,
∴∠CDE=∠ADG,
又∵EF⊥AC,
∴∠AEF=90°-∠CAD=45°,
∴∠DEG=∠AEF=45°,
在Rt△EDG中,∠DGE=90°-∠DEG=45°,
∴∠DGE=∠DEG,
∴ED=GD
在△ADG与△CDE中,
$\left\{\begin{array}{l}{ED=GD}\\{∠CDE=∠ADG}\\{CD=AD}\end{array}\right.$,
∴△ADG≌△CDE(SAS);
(2)∵CE平分∠ACD,
∴∠ACE=∠ECG,
又∵EF⊥AC,AD⊥CD,
∴ED=EF,
∴EF=AF=DE=DG,
设DG为k,则ED=k,AE=$\sqrt{2}$k,AD=AE+ED=($\sqrt{2}$+1)k,
tan∠AGD=$\frac{AD}{DG}=\frac{(\sqrt{2}+1)k}{k}$=$\sqrt{2}$+1
点评 此题考查正方形的性质,关键是利用全等三角形的判定和性质解答.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
4.若一元二次方程x2+2x+a=0的有实数解,则a的取值范围是( )
| A. | a<1 | B. | a≤4 | C. | a≤1 | D. | a≥1 |
5.已知x,y是二元一次方程式组$\left\{\begin{array}{l}{2x+y=10}\\{2y-x=6}\end{array}\right.$的解,则3x-y的算术平方根为( )
| A. | ±2 | B. | 4 | C. | $\sqrt{2}$ | D. | 2 |
2.下面四个图形是多面体的展开图,其中不是棱柱的展开图的是( )
| A. | 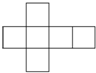 | B. | 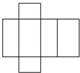 | C. | 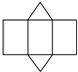 | D. | 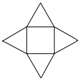 |
20.(-2)+3的值等于( )
| A. | -5 | B. | -1 | C. | -6 | D. | 1 |
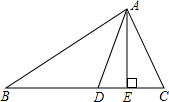 如图,AE、AD分别是△ABC的高和角平分线,且∠B=36°,∠C=66°,求∠DAE的度数.
如图,AE、AD分别是△ABC的高和角平分线,且∠B=36°,∠C=66°,求∠DAE的度数.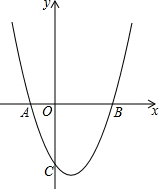 如图,抛物线y=x2-2x+k与x轴交于A,B两点,与y轴交于C(0,-3).
如图,抛物线y=x2-2x+k与x轴交于A,B两点,与y轴交于C(0,-3).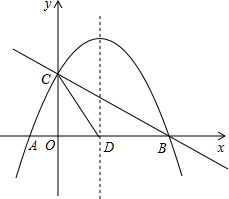 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2). 已知,如图AB=AC,CD⊥AB于D,BE⊥AC于E,BE和CD相交于点O,求证:AO平分∠BAC.
已知,如图AB=AC,CD⊥AB于D,BE⊥AC于E,BE和CD相交于点O,求证:AO平分∠BAC.