题目内容
9.先化简,再求值:$\frac{{a}^{2}-{b}^{2}}{a}$÷(a-$\frac{2ab-{b}^{2}}{a}$),其中a=2+$\sqrt{3}$,b=2-$\sqrt{3}$.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则计算,约分得到最简结果,把a与b的值代入计算即可求出值.
解答 解:原式=$\frac{(a+b)(a-b)}{a}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$=$\frac{(a+b)(a-b)}{a}$•$\frac{a}{(a-b)^{2}}$=$\frac{a+b}{a-b}$,
当a=2+$\sqrt{3}$,b=2-$\sqrt{3}$时,原式=$\frac{2+\sqrt{3}+2-\sqrt{3}}{2+\sqrt{3}-2+\sqrt{3}}$=$\frac{4}{2\sqrt{3}}$=$\frac{2\sqrt{3}}{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
19.计算8+6÷(-2)的结果是( )
| A. | -7 | B. | -5 | C. | 5 | D. | 7 |
20.已知一组数据:-3,6,2,-1,0,4,则这组数据的中位数是( )
| A. | 1 | B. | $\frac{4}{3}$ | C. | 0 | D. | 2 |
17.小明在”百度”搜索引擎中输入”钓鱼岛最新消息”,能搜索到与之相关的结果个数约为564000,这个数用科学记数法表示为( )
| A. | 5.64×104 | B. | 56.4×104 | C. | 5.64×105 | D. | 0.564×106 |
4.若一元二次方程x2+2x+a=0的有实数解,则a的取值范围是( )
| A. | a<1 | B. | a≤4 | C. | a≤1 | D. | a≥1 |
14.下列选项中,显示部分在总体中所占百分比的统计图是( )
| A. | 扇形图 | B. | 条形图 | C. | 折线图 | D. | 直方图 |
18.点P(4,3)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
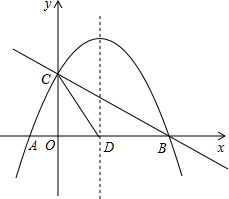 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).