题目内容
19.计算$\sqrt{12}+(\sqrt{3}-π{)^0}$=2$\sqrt{3}+1$.分析 首先根据算术平方根的计算方法,求出$\sqrt{12}$的值是多少;然后根据a0=1(a≠0),求出${(\sqrt{3}-π)}^{0}$的值是多少;最后再求和,求出算式$\sqrt{12}+(\sqrt{3}-π{)^0}$的值是多少即可.
解答 解:$\sqrt{12}+(\sqrt{3}-π{)^0}$=2$\sqrt{3}+1$.
故答案为:2$\sqrt{3}+1$.
点评 (1)此题主要考查了平方根的性质和应用,要熟练掌握,解答此题的关键是要明确:一个正数有两个平方根,这两个平方根互为相反数,零的平方根是零,负数没有平方根.
(2)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:(1)a0=1(a≠0);(2)00≠1.

练习册系列答案
相关题目
9.南京青奥会期间约有1020000人次参与了青奥文化教育活动.将数据1020000用科学记数法表示为( )
| A. | 10.2×105 | B. | 1.02×105 | C. | 1.02×106 | D. | 1.02×107 |
7.-$\frac{2}{5}$的相反数是( )
| A. | -$\frac{5}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{2}{5}$ | D. | -$\frac{2}{5}$ |
4.若一元二次方程x2+2x+a=0的有实数解,则a的取值范围是( )
| A. | a<1 | B. | a≤4 | C. | a≤1 | D. | a≥1 |
11.a的相反数是( )
| A. | |a| | B. | $\frac{1}{a}$ | C. | -a | D. | $\sqrt{a}$ |
8.把代数式3x3-12x2+12x分解因式,结果正确的是( )
| A. | 3x(x2-4x+4) | B. | 3x(x-4)2 | C. | 3x(x+2)(x-2) | D. | 3x(x-2)2 |
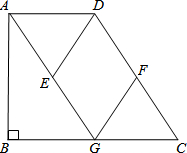 如图.在直角梯形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.
如图.在直角梯形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.