题目内容
11．若正比例函数y=（2m-1）${x}^{2-{m}^{2}}$中，y随x的增大而减少（1）求这个正比例函数的解析式；
（2）当x=$\frac{1}{4}$时，求y的值．
分析 （1）根据正比例函数的自变量的指数为1且比例系数不为零即可求得m的值，代入求得解析式即可；
（2）将x的值代入求得的解析式即可求得y的值．
解答 解：（1）∵正比例函数y=（2m-1）${x}^{2-{m}^{2}}$中，y随x的增大而减少，
∴$\left\{\begin{array}{l}{2-{m}^{2}=1}\\{2m-1＜0}\end{array}\right.$，
解得：m=-1，
∴正比例函数为y=-3x；
（2）当x=$\frac{1}{4}$时，y=-3×$\frac{1}{4}$=-$\frac{3}{4}$．
点评 本题考查了待定系数法求正比例函数的解析式，解题的关键是根据函数的增减性确定反比例函数的系数的符号，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
2．
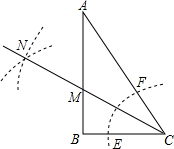Rt△ABC中，∠B=90°∠A=30°．以C为圆心，小于BC长为半径画弧与AC、BC边交于点F、E．分别以E、F为圆心，大于$\frac{1}{2}$EF为半径画弧，两弧交于点N，若BC=$\sqrt{3}$，则点M到AC的距离是（ ）
Rt△ABC中，∠B=90°∠A=30°．以C为圆心，小于BC长为半径画弧与AC、BC边交于点F、E．分别以E、F为圆心，大于$\frac{1}{2}$EF为半径画弧，两弧交于点N，若BC=$\sqrt{3}$，则点M到AC的距离是（ ）| A． | 1 | B． | $\sqrt{3}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | 3 |
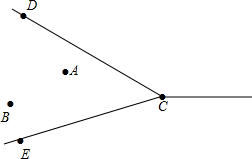A、B两村坐落在两条相交公路CD、CE内，现计划修建一所小学校，要求学校必须满足下列条件：